题目内容
设Sn是正项数列B的前n项和,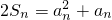 .
.
(Ⅰ)求证数列{an}是等差数列,并求{an}的通项公式;
(Ⅱ)已知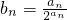 ,求{bn}的前n项和Tn.
,求{bn}的前n项和Tn.
解:(Ⅰ)由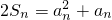 .
.
当n=1时,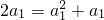 ,又a1>0,解得a1=1.
,又a1>0,解得a1=1.
当n≥2时, ,
,
∴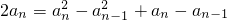 ,
,
∴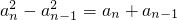 ,
,
∴(an+an-1)(an-an-1-1)=0,
∵an+an-1>0,
∴an-an-1=1
则数列{an}是以1为首项,1为公差的等差数列
∴an=a1+(n-1)d=1+(n-1)=n.
(Ⅱ)∵ ,
,
∴ ①
①
又因为 ②
②
①-②得: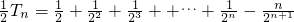
=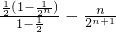
=
=
所以 .
.
分析:(Ⅰ)由给出的数列的递推式,取n=1时,求出a1,取n=n-1写出第二个递推式,两式相减后整理,得到an-an-1=1,即可证明数列{an}是等差数列;
(Ⅱ)把(Ⅰ)中求出的{an}的通项公式代入bn,然后利用错位相减法求数列{bn}的前n项和Tn.
点评:本题考查了等差数列的通项公式,考查了利用错位相减法求数列的前n项和,由一个等差数列和一个等比数列的积构成的数列,求其前n项和,一般是借助于错位相减法,此题是中档题.
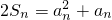 .
.当n=1时,
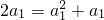 ,又a1>0,解得a1=1.
,又a1>0,解得a1=1.当n≥2时,
 ,
,∴
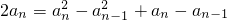 ,
,∴
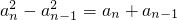 ,
,∴(an+an-1)(an-an-1-1)=0,
∵an+an-1>0,
∴an-an-1=1
则数列{an}是以1为首项,1为公差的等差数列
∴an=a1+(n-1)d=1+(n-1)=n.
(Ⅱ)∵
 ,
,∴
 ①
①又因为
 ②
②①-②得:
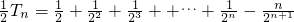
=
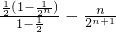
=

=

所以
 .
.分析:(Ⅰ)由给出的数列的递推式,取n=1时,求出a1,取n=n-1写出第二个递推式,两式相减后整理,得到an-an-1=1,即可证明数列{an}是等差数列;
(Ⅱ)把(Ⅰ)中求出的{an}的通项公式代入bn,然后利用错位相减法求数列{bn}的前n项和Tn.
点评:本题考查了等差数列的通项公式,考查了利用错位相减法求数列的前n项和,由一个等差数列和一个等比数列的积构成的数列,求其前n项和,一般是借助于错位相减法,此题是中档题.

练习册系列答案
相关题目




