题目内容
((本小题满分12分)
如图,四棱锥S=ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=a,点E是SD上的点,且DE=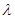 a(0<
a(0<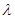 ≦1).
≦1).
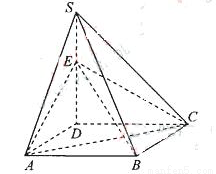
(Ⅰ)求证:对任意的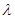
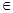 (0、1),都有AC⊥BE:
(0、1),都有AC⊥BE:
(Ⅱ)若二面角C-AE-D的大小为600C,求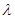 的值。
的值。
【答案】
(Ⅰ)连接BD,由底面是正方形可得AC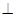 BD。
BD。
又 SD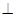 平面ABCD,
平面ABCD,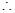 BD是BE在平面ABCD上的射影,
BD是BE在平面ABCD上的射影,
由三垂线定理得AC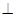 BE.
BE.
(II) 由SD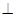 平面ABCD,CD
平面ABCD,CD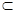 平面ABCD,
平面ABCD,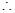 SD
SD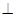 CD.
CD.
又底面ABCD是正方形,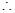 CD
CD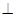 AD,又SD
AD,又SD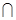 AD=D,
AD=D,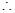 CD
CD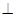 平面SAD。
平面SAD。
过点D在平面SAD内做DF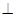 AE于F,连接CF,则CF
AE于F,连接CF,则CF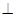 AE,
AE,
故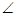 CFD是二面角C-AE-D 的平面角,即
CFD是二面角C-AE-D 的平面角,即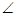 CFD=60°
CFD=60°
在Rt△ADE中,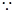 AD=
AD=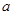 , DE=
, DE= 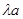 , AE=
, AE=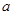
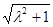 。
。
于是,DF=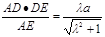
在Rt△CDF中,由 cot60°=
cot60°=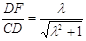
得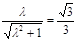 ,
即
,
即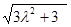 =3
=3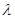
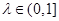 , 解得
, 解得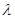 =
=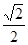
【解析】略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目