题目内容
如下图,用A、B、C三类不同的元件连接两个系统N1,N2,当元件A、B、C都正常工作时系统N1正常工作,当元件A正常工作且元件B、C至少有一个正常工作时系统N2正常工作,已知元件A、B、C正常工作的概率分别为0.80,0.90,0.90,分别求系统N1,N2正常工作的概率p1,p2.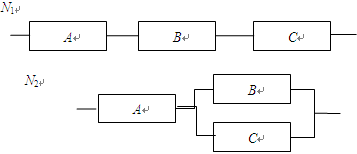

(1)P1=" 0.648." (2)P2=" 0.792."
试题分析:分别记元件A,B,C正常工作的时间为事件A,B,C,由已知条件P(A)=0.8,P(B)=0.9,P(C)=0.9,
(1)因为事件A,B,C是相互独立的,所以P1=P(ABC)=P(A)P(B)P(C)=0.648,
系统N1正常工作的概率是0.648. 6分
(2)P2=
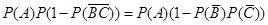 =0.792
=0.792系统N2正常工作的概率是0.792. 12分
点评:注意体会解决概率应用题的思考方法,正向思考时要善于将较复杂的问题进行分解,解决有些问题时还要学会运用逆向思考的方法

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目

 A
A
 A
A 是必然事件
是必然事件 是必然事件
是必然事件 一定不互斥
一定不互斥 与
与 可能互斥也可能不互斥
可能互斥也可能不互斥