题目内容
如图所示,在三棱锥P—ABC中,PA⊥平面ABC,AB=BC=CA=2,M为AB的中点,四点P、A、M、C都在球O的球面上.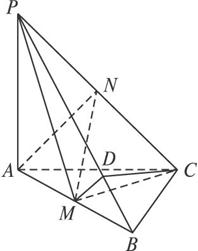
(1)证明平面PAB⊥平面PCM;
(2)证明线段PC的中点为球O的球心;
(3)若球O的表面积为20π,求二面角A-PB-C的平面角的余弦值.
(1)证明:∵AC=BC,M为AB的中点,
∴CM⊥AB.
∵PA⊥平面ABC,CM![]() 平面ABC,
平面ABC,
∴PA⊥CM
∵AB∩PA=A,AB![]() 平面PAB,PA
平面PAB,PA![]() 平面PAB,
平面PAB,
∴CM⊥平面PAB.
∵CM![]() 平面PCM,
平面PCM,
∴平面PAB⊥平面PCM.
(2)证明:由(1)知CM⊥平面PAB.

∵PM![]() 平面PAB,
平面PAB,
∴CM⊥PM.
∵PA⊥平面ABC,AC![]() 平面ABC,
平面ABC,
∴PA⊥AC.
取PC的中点N,连结MN、AN.
在Rt△PAC中,点N为斜边PC的中点,
∴AN=PN=NC.
在Rt△PMC中,点N为斜边PC的中点,
∴MN=PN=NC.
∴PN=NC=AN=MN.
∴点N是球O的球心,即线段PC的中点为球O的球心.
(3)解法一:依题意得4π·NC2=20π,解得NC=![]() .
.
∴PC=2![]() ,PA=
,PA=![]() =4.
=4.
作MD⊥PB,垂足为D,连结CD.
由(1)知CM⊥平面PAB.
∵PB![]() 平面PAB,∴PB⊥CM.
平面PAB,∴PB⊥CM.
∵MD∩MC=M,∴PB⊥平面CMD.
∵CD![]() 平面CMD,∴CD⊥PB.
平面CMD,∴CD⊥PB.
∴∠CDM是二面角APBC的平面角.
在Rt△PAB和Rt△MDB中,PB=![]() =
=![]() =2
=2![]() ,
,![]() =
=![]() .∴MD=
.∴MD=![]() .
.
在Rt△CMD中,CD=![]() =
=![]() ,
,
cos∠CDM=![]() =
=![]() .
.
∴二面角A-PB-C的平面角的余弦值是![]() .
.
解法二:依题意得4π·NC2=20π,解得NC=![]() .
.
∴PC=2![]() ,PA=
,PA=![]() =4.
=4.
如图,建立空间直角坐标系A—xyz,

则A(0,0,0),M(![]() ,
,![]() ,0),C(0,2,0),B(
,0),C(0,2,0),B(![]() ,1,0),P(0,0,4).∴
,1,0),P(0,0,4).∴![]() =(
=(![]() ,
,![]() ,0),
,0),
![]() =(3,-1,0),
=(3,-1,0),![]() =(0,-2,4).
=(0,-2,4).
由(1)知![]() 是平面PAB的一个法向量.
是平面PAB的一个法向量.
设平面PBC的法向量n的坐标为(x,y,z),
由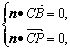 得
得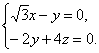
令x=2,得y=2![]() ,z=
,z=![]() .
.
∴平面PBC的一个法向量为n=(2,2![]() ,
,![]() ).
).
∴cos〈n,![]() 〉=
〉=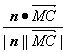
=
=![]() .
.
∴二面角A-PB-C的平面角的余弦值是![]() .
.

 (2012•广州一模)如图所示,在三棱锥P-ABC中,
(2012•广州一模)如图所示,在三棱锥P-ABC中, 如图所示,在三棱锥P-ABC中,PA⊥面ABC,∠ABC=90°.该三棱锥中有哪些直角三角形,哪些面面垂直(只写结果,不要求证明).
如图所示,在三棱锥P-ABC中,PA⊥面ABC,∠ABC=90°.该三棱锥中有哪些直角三角形,哪些面面垂直(只写结果,不要求证明). 如图所示,在三棱锥P-ABC中,PA⊥面ABC,∠ABC=90°.
如图所示,在三棱锥P-ABC中,PA⊥面ABC,∠ABC=90°. 如图所示,在三棱锥P-ABC中,
如图所示,在三棱锥P-ABC中, 如图所示,在三棱锥P-ABC中,PA⊥平面ABC,PA=1,AB⊥AC,AB=AC=2,E为AC的中点.
如图所示,在三棱锥P-ABC中,PA⊥平面ABC,PA=1,AB⊥AC,AB=AC=2,E为AC的中点.