题目内容
已知点B(0,1),A,C为椭圆C:
+y2=1(a>1)上的两点,△ABC是以B为直角顶点的直角三角形.
(I)当a=4时,求线段BC的中垂线l在x轴上截距的取值范围.
(II)△ABC能否为等腰三角形?若能,这样的三角形有几个?
| x2 | a2 |
(I)当a=4时,求线段BC的中垂线l在x轴上截距的取值范围.
(II)△ABC能否为等腰三角形?若能,这样的三角形有几个?
分析:(I)依题意,可知椭圆的方程为:
+y2=1,设C(4cosθ,sinθ),可求得直线l的方程为y=-
x+
+
,令y=0得x=
=
cosθ(cosθ≠0),利用余弦cosθ的有界性即可求得线段BC的中垂线l在x轴上截距的取值范围;
(II)当等腰直角三角形ABC的两条腰AB与BC不关于y轴对称时,设出AB的方程为y=kx+1(k>0),BC的方程为y=-
x+1,利用直线与方程与椭圆方程联立,利用等腰直角三角形ABC中的两腰|AB|=|BC|,借助基本不等式即可求得a的取值范围;同理可求两条腰AB与BC关于y轴对称时a的取值范围.
| x2 |
| 42 |
| 4cosθ |
| sinθ-1 |
| 8cos2θ |
| sinθ-1 |
| 1+sinθ |
| 2 |
| 15cos2θ |
| 8cosθ |
| 15 |
| 8 |
(II)当等腰直角三角形ABC的两条腰AB与BC不关于y轴对称时,设出AB的方程为y=kx+1(k>0),BC的方程为y=-
| 1 |
| k |
解答:解:(I)∵a=4,
∴椭圆的方程为:
+y2=1,故B(0,1),
设C(4cosθ,sinθ),
则BC的中点M(2cosθ,
),
∵BC的斜率kBC=
,
∴线段BC的中垂线l的斜率k=-
=-
,
∴直线l的方程为:y-
=-
(x-2cosθ),
∴y=-
x+
+
,
令y=0得:x=
=
cosθ(cosθ≠0)
∵-1≤cosθ≤1且cosθ≠0,
∴-
≤x=
cosθ≤
且x≠0,
∴线段BC的中垂线l在x轴上截距的取值范围为[-
,0)∪(0,
].
(II)当等腰直角三角形ABC的两条腰AB与BC不关于y轴对称时,作图如右,
 设此时过B(0,1)的AB的方程为y=kx+1(k>0),则BC的方程为y=-
设此时过B(0,1)的AB的方程为y=kx+1(k>0),则BC的方程为y=-
x+1,
由
得:(a2k2+1)x2+2a2kx=0,
设该方程两根为x1,x2,则x1+x2=-
,x1x2=0,
则|AB|=
=|x1-x2|•
=
•
=
•|
|,
同理可求,|BC|=
•|
|=
•|
|,
∵|AB|=|BC|,
∴
•|
|=
•|
|,
约分后整理得:k3-a2k2+a2k-1=0,
即a2k(k-1)=(k-1)(k2+k+1),
当k=1时,AB的方程为y=x+1,BC的方程为y=-x+1,此时两直线关于y轴对称,与所设不符,故k≠1;
∴a2=
=k+
+1≥3(当且仅当k=1时取等号),又k≠1,
∴a2>3,
∴a>
,即当a>
时,如图的不关于y轴对称等腰直角三角形ABC存在,
又不关于y轴对称的还有另一个,关于y轴对称的必有一个,
因此,当a>
时,以B为直角顶点的等腰三角ABC共三个.
当1<a≤
时,以B为直角顶点的等腰三角ABC只有一个,此时两腰关于y轴对称.
∴椭圆的方程为:
| x2 |
| 42 |
设C(4cosθ,sinθ),
则BC的中点M(2cosθ,
| 1+sinθ |
| 2 |
∵BC的斜率kBC=
| sinθ-1 |
| 4cosθ |
∴线段BC的中垂线l的斜率k=-
| 1 |
| kBC |
| 4cosθ |
| sinθ-1 |
∴直线l的方程为:y-
| 1+sinθ |
| 2 |
| 4cosθ |
| sinθ-1 |
∴y=-
| 4cosθ |
| sinθ-1 |
| 8cos2θ |
| sinθ-1 |
| 1+sinθ |
| 2 |
令y=0得:x=
| 15cos2θ |
| 8cosθ |
| 15 |
| 8 |
∵-1≤cosθ≤1且cosθ≠0,
∴-
| 15 |
| 8 |
| 15 |
| 8 |
| 15 |
| 8 |
∴线段BC的中垂线l在x轴上截距的取值范围为[-
| 15 |
| 8 |
| 15 |
| 8 |
(II)当等腰直角三角形ABC的两条腰AB与BC不关于y轴对称时,作图如右,
 设此时过B(0,1)的AB的方程为y=kx+1(k>0),则BC的方程为y=-
设此时过B(0,1)的AB的方程为y=kx+1(k>0),则BC的方程为y=-| 1 |
| k |
由
|
设该方程两根为x1,x2,则x1+x2=-
| 2a2k |
| a2k2+1 |
则|AB|=
| (x2-x1)2+(y2-y1)2 |
=|x1-x2|•
| 1+k2 |
=
| 1+k2 |
| (x2+x1)2-4x1x2 |
=
| 1+k2 |
| 2a2k |
| a2k2+1 |
同理可求,|BC|=
1+
|
2a2(-
| ||
|
| ||
| |k| |
| 2a2k |
| a2+k2 |
∵|AB|=|BC|,
∴
| 1+k2 |
| 2a2k |
| a2k2+1 |
| ||
| |k| |
| 2a2k |
| a2+k2 |
约分后整理得:k3-a2k2+a2k-1=0,
即a2k(k-1)=(k-1)(k2+k+1),
当k=1时,AB的方程为y=x+1,BC的方程为y=-x+1,此时两直线关于y轴对称,与所设不符,故k≠1;
∴a2=
| k2+k+1 |
| k |
| 1 |
| k |
∴a2>3,
∴a>
| 3 |
| 3 |
又不关于y轴对称的还有另一个,关于y轴对称的必有一个,
因此,当a>
| 3 |
当1<a≤
| 3 |
点评:本题考查椭圆的性质,着重考查椭圆的参数方程的应用,考查直线的点斜式、截距的综合应用,突出考查直线与圆锥曲线的位置关系,考查转化思想、方程思想、分类讨论思想的综合应用,考查逻辑思维、创新思维、综合运算能力,属于难题.

练习册系列答案
相关题目
 的切线(P点不在y轴上).
的切线(P点不在y轴上).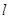 与(I)中的抛物线相交于M、N两点,问是否存在定点R,使
与(I)中的抛物线相交于M、N两点,问是否存在定点R,使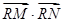 为常数?若存在,求出点R的坐标与常数;若不存在,请说明理由。
为常数?若存在,求出点R的坐标与常数;若不存在,请说明理由。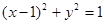 的切线(P点不在y轴上)
的切线(P点不在y轴上) 与(I)中的抛物线相交于M、N两点,问是否存在定点R,使
与(I)中的抛物线相交于M、N两点,问是否存在定点R,使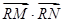 为常数?若存在,求出点R的坐标与常数;若不存在,请说明理由。
为常数?若存在,求出点R的坐标与常数;若不存在,请说明理由。