题目内容
已知点B(0,1),点C(0,—3),直线PB、PC都是圆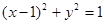 的切线(P点不在y轴上)
的切线(P点不在y轴上)
(I)求过点P且焦点在x轴上抛物线的标准方程;
(II)过点(1,0)作直线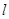 与(I)中的抛物线相交于M、N两点,问是否存在定点R,使
与(I)中的抛物线相交于M、N两点,问是否存在定点R,使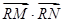 为常数?若存在,求出点R的坐标与常数;若不存在,请说明理由。
为常数?若存在,求出点R的坐标与常数;若不存在,请说明理由。
【答案】
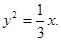 ,存在定点R(0,0),相应的常数是
,存在定点R(0,0),相应的常数是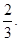
【解析】解:(I)设直线PC的方程为: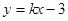 ,
,
由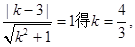 所以PC的方程为
所以PC的方程为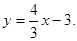 …………3分
…………3分
由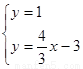 得P点的坐标为(3,1)。
得P点的坐标为(3,1)。
可求得抛物线的标准方程为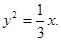 ………………6分
………………6分
(II)设直线l的方程为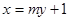 ,代入抛物线方程并整理得
,代入抛物线方程并整理得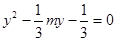
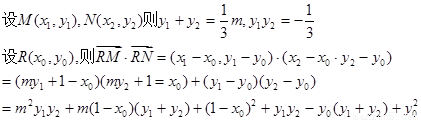
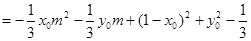 ………………11分
………………11分
当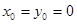 时上式是一个与m无关的常数
时上式是一个与m无关的常数
所以存在定点R(0,0),相应的常数是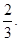 ………………13分
………………13分

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
 的切线(P点不在y轴上).
的切线(P点不在y轴上).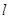 与(I)中的抛物线相交于M、N两点,问是否存在定点R,使
与(I)中的抛物线相交于M、N两点,问是否存在定点R,使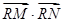 为常数?若存在,求出点R的坐标与常数;若不存在,请说明理由。
为常数?若存在,求出点R的坐标与常数;若不存在,请说明理由。