题目内容
 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1,F分别是棱AD,AA1,AB的中点.
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1,F分别是棱AD,AA1,AB的中点.(1)证明:直线EE1∥平面FCC1;
(2)求二面角B-FC1-C的余弦值.
分析:(1)可以通过证明面面平行来证明线面平行;
(2)通过建立空间直角坐标系,先求出两个平面的法向量,则两个平面的法向量的夹角即为两平面的二面角或其补角.
(2)通过建立空间直角坐标系,先求出两个平面的法向量,则两个平面的法向量的夹角即为两平面的二面角或其补角.
解答:解:(1)∵F为AB的中点,CD=2,AB=4,AB∥CD,∴CD∥AF,
∴四边形AFCD为平行四边形,∴AD∥FC.
又CC1∥DD1,FC∩CC1=C,FC?平面FCC1,CC1?平面FCC1,
∴平面ADD1A1∥平面FCC1,
又EE1?平面ADD1A1,∴EE1∥平面FCC1.
(2)过D作DR⊥CD交于AB于R,以D为坐标原点建立如图所示的空间直角坐标系.
则F(
,1,0),B(
,3,0),C(0,2,0),C1(0,2,2),
∴
=(0,2,0),
=(-
,-1,2),
=(
,3,0).
由FB=CB=CD=DF,∴四边形BCEF是菱形,∴DB⊥FC.
又CC1⊥平面ABCD,
∴
为平面FCC1的一个法向量.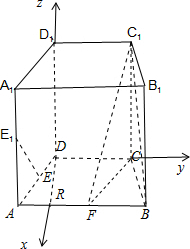
设平面BFC1的一个法向量为
=(x,y,z),
则
得
,可得y=0,令x=2,则z=
,∴
=(2,0,
).
∴cos<
,
>=
=
=
.
故所求二面角的余弦值为
.

∴四边形AFCD为平行四边形,∴AD∥FC.
又CC1∥DD1,FC∩CC1=C,FC?平面FCC1,CC1?平面FCC1,
∴平面ADD1A1∥平面FCC1,
又EE1?平面ADD1A1,∴EE1∥平面FCC1.
(2)过D作DR⊥CD交于AB于R,以D为坐标原点建立如图所示的空间直角坐标系.
则F(
| 3 |
| 3 |
∴
| FB |
| BC1 |
| 3 |
| DB |
| 3 |
由FB=CB=CD=DF,∴四边形BCEF是菱形,∴DB⊥FC.
又CC1⊥平面ABCD,
∴
| DB |

设平面BFC1的一个法向量为
| n |
则
|
|
| 3 |
| n |
| 3 |
∴cos<
| n |
| DB |
| ||||
|
|
2
| ||||||||
|
| ||
| 7 |
故所求二面角的余弦值为
| ||
| 7 |
点评:熟练掌握利用面面平行来证明线面平行、利用两个平面的法向量的夹角求两平面的二面角是解题的关键..

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
 18、如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1分别是棱AD,AA1的中点,F为AB的中点.证明:
18、如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1分别是棱AD,AA1的中点,F为AB的中点.证明: 18、如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1分别是棱AD,AA1的中点.
18、如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1分别是棱AD,AA1的中点. 15、如图,在直四棱柱ABCD-A1B1C1D1中,A1C1⊥B1D1,E,F分别是AB,BC的中点.
15、如图,在直四棱柱ABCD-A1B1C1D1中,A1C1⊥B1D1,E,F分别是AB,BC的中点. (2010•抚州模拟)如图,在直四棱柱ABCD-A1B1C1D1中,AB=BC,∠ABC=60°,BB1=BC=2,M为BC中点,点N在CC1上.
(2010•抚州模拟)如图,在直四棱柱ABCD-A1B1C1D1中,AB=BC,∠ABC=60°,BB1=BC=2,M为BC中点,点N在CC1上.