题目内容
(本小题满分14分)已知函数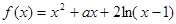 ,
,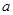 是常数.
是常数.
(Ⅰ) 证明曲线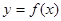 在点
在点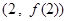 的切线经过
的切线经过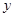 轴上一个定点;
轴上一个定点;
(Ⅱ) 若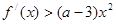 对
对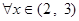 恒成立,求
恒成立,求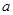 的取值范围;
的取值范围;
(参考公式: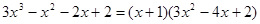 )
)
(Ⅲ)讨论函数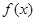 的单调区间.
的单调区间.
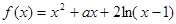 ,
,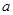 是常数.
是常数.(Ⅰ) 证明曲线
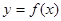 在点
在点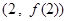 的切线经过
的切线经过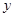 轴上一个定点;
轴上一个定点;(Ⅱ) 若
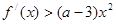 对
对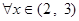 恒成立,求
恒成立,求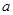 的取值范围;
的取值范围;(参考公式:
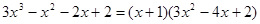 )
)(Ⅲ)讨论函数
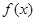 的单调区间.
的单调区间.(1)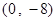 ;(2)
;(2)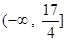 ;(3)单调增区间是
;(3)单调增区间是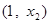 和
和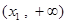 ,单调减区间是
,单调减区间是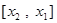 .
.
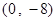 ;(2)
;(2)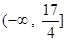 ;(3)单调增区间是
;(3)单调增区间是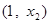 和
和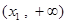 ,单调减区间是
,单调减区间是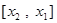 .
.(1)利用导数求出斜率,然后写出点斜式方程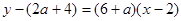 ,从而可看出当x=0时,切线经过y轴上的定点(0,-8).
,从而可看出当x=0时,切线经过y轴上的定点(0,-8).
(II)由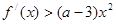 得
得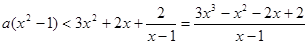 ……5分,
……5分,
对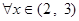 ,
,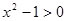 ,所以
,所以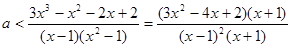
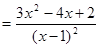 ,然后再构造函数
,然后再构造函数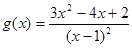 ,利用导数研究其最小值即可.
,利用导数研究其最小值即可.
(III)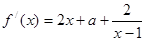
=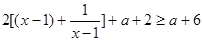 ,然后再对
,然后再对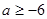 和
和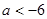 两种情况进行讨论。
两种情况进行讨论。
解:⑴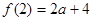 ,
,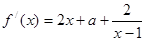 ,……1分
,……1分 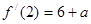 ……2分,
……2分,
曲线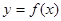 在点
在点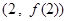 的切线为
的切线为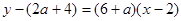 ……3分,
……3分,
当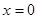 时,由切线方程得
时,由切线方程得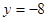 ,所以切线经过
,所以切线经过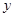 轴上的定点
轴上的定点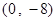 ……4分.
……4分.
⑵由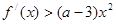 得
得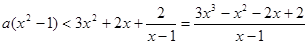 ……5分,
……5分,
对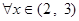 ,
,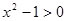 ,所以
,所以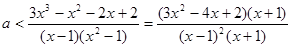
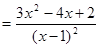 ……6分,
……6分,
设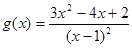 ,则
,则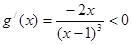 ……7分,
……7分,
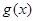 在区间
在区间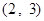 单调递减……8分,
单调递减……8分,
所以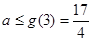 ,
,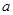 的取值范围为
的取值范围为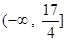 ……9分.
……9分.
⑶函数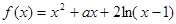 的定义域为
的定义域为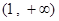 ,
,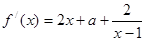
=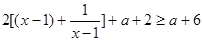 ……10分.
……10分.
若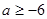 ,则
,则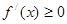 ,
,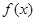 在定义域
在定义域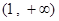 上单调增加……11分;
上单调增加……11分;
若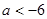 ,解方程
,解方程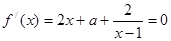 得
得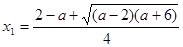 ,
,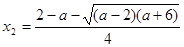 ……12分,
……12分,
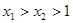 ,当
,当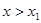 或
或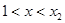 时,
时,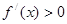 ;
;
当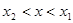 时,
时,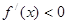 ……13分,
……13分,
所以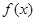 的单调增区间是
的单调增区间是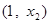 和
和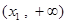 ,单调减区间是
,单调减区间是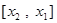 (区间无论包含端点
(区间无论包含端点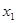 、
、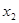 均可,但要前后一致)……14分
均可,但要前后一致)……14分
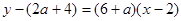 ,从而可看出当x=0时,切线经过y轴上的定点(0,-8).
,从而可看出当x=0时,切线经过y轴上的定点(0,-8).(II)由
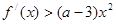 得
得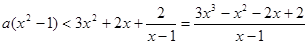 ……5分,
……5分,对
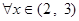 ,
,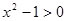 ,所以
,所以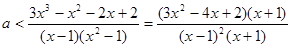
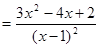 ,然后再构造函数
,然后再构造函数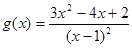 ,利用导数研究其最小值即可.
,利用导数研究其最小值即可.(III)
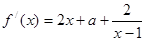
=
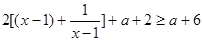 ,然后再对
,然后再对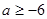 和
和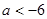 两种情况进行讨论。
两种情况进行讨论。解:⑴
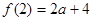 ,
,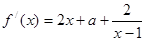 ,……1分
,……1分 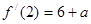 ……2分,
……2分,曲线
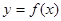 在点
在点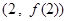 的切线为
的切线为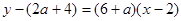 ……3分,
……3分,当
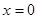 时,由切线方程得
时,由切线方程得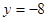 ,所以切线经过
,所以切线经过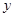 轴上的定点
轴上的定点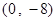 ……4分.
……4分.⑵由
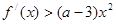 得
得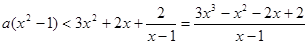 ……5分,
……5分,对
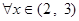 ,
,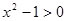 ,所以
,所以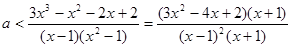
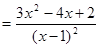 ……6分,
……6分,设
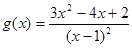 ,则
,则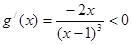 ……7分,
……7分,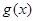 在区间
在区间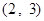 单调递减……8分,
单调递减……8分,所以
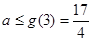 ,
,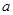 的取值范围为
的取值范围为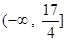 ……9分.
……9分.⑶函数
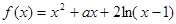 的定义域为
的定义域为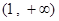 ,
,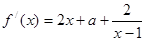
=
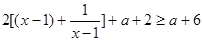 ……10分.
……10分.若
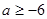 ,则
,则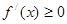 ,
,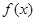 在定义域
在定义域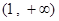 上单调增加……11分;
上单调增加……11分;若
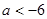 ,解方程
,解方程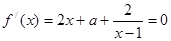 得
得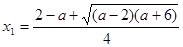 ,
,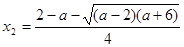 ……12分,
……12分,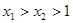 ,当
,当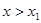 或
或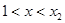 时,
时,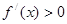 ;
;当
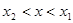 时,
时,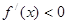 ……13分,
……13分,所以
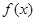 的单调增区间是
的单调增区间是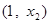 和
和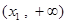 ,单调减区间是
,单调减区间是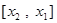 (区间无论包含端点
(区间无论包含端点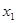 、
、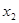 均可,但要前后一致)……14分
均可,但要前后一致)……14分
练习册系列答案
相关题目
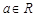 ,函数
,函数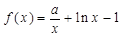 ,
,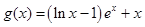 (其中
(其中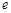 为自然对数的底数).
为自然对数的底数).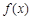 在
在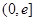 上的单调性;
上的单调性;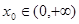 ,使曲线
,使曲线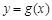 在点
在点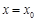 处的切线与
处的切线与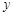 轴垂直? 若存在,
轴垂直? 若存在,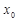 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;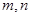 满足
满足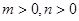 ,求证:
,求证: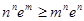 .
.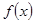 的定义域为
的定义域为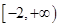 ,部分对应值如下表,
,部分对应值如下表,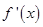 为
为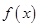 的导函数,函数
的导函数,函数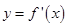 的图象如图所示.若实数
的图象如图所示.若实数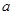 满足
满足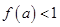 ,则
,则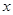
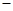 2
2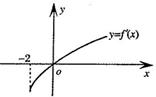
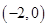 B.
B.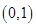 C.
C.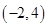 D.
D.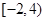
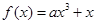 在定义域
在定义域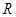 上恰有三个单调区间,则
上恰有三个单调区间,则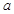 的取值范围是( )
的取值范围是( )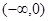
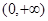
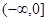
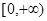
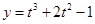 ,当
,当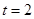 s时,物体的瞬时速度v等于 ( )
s时,物体的瞬时速度v等于 ( )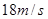
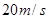
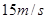
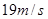
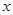 月,商品A的价格
月,商品A的价格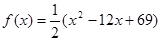 (
(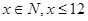 ,价格单位:元),且第
,价格单位:元),且第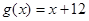 (单位:万件).(1)2011年的最低价格是多少?(2)2011年的哪一个月的销售收入最少?
(单位:万件).(1)2011年的最低价格是多少?(2)2011年的哪一个月的销售收入最少?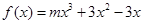 ,
,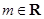 .
.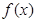 在
在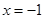 处取得极值,试求
处取得极值,试求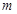 的值,并求
的值,并求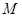
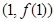 处的切线方程;
处的切线方程;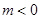 ,若函数
,若函数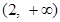 上存在单调递增区间,求
上存在单调递增区间,求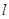 与函数f(x)=x3图像相切,且
与函数f(x)=x3图像相切,且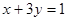 垂直,则直线
垂直,则直线 在点(0,1)处的切线方程为
在点(0,1)处的切线方程为


