题目内容
3.如图,已知等腰梯形ABCD中,AD∥BC,AB=AD=$\frac{1}{2}$BC=2,E是BC的中点,AE∩BD=M,将△BAE沿着AE翻折成△B1AE,使平面B1AE⊥平面AECD.
(Ⅰ) 求证:CD⊥平面B1DM;
(Ⅱ)求二面角D-AB1-E的余弦值;
(Ⅲ)在线段B1C上是否存在点P,使得MP∥平面B1AD,若存在,求出$\frac{{{B_1}P}}{{{B_1}C}}$的值;若不存在,说明理由.
分析 (Ⅰ)证明CD⊥DM.B1M⊥CD.通过直线与平面垂直的判定定理证明CD⊥平面B1MD.
(Ⅱ)以ME为x轴,MD为y轴,MB1为z轴建立空间直角坐标系,求出平面AB1E的法向量,平面DB1A的法向量通过向量的数量积求解二面角D-AB1-E的余弦值.
(Ⅲ) 存在点P,使得MP∥平面B1AD,法一:取线段B1C中点P,B1D中点Q,连结MP,PQ,AQ.
证明$MP\underline{\underline{∥}}AQ$.说明MP∥平面AB1D.得到结果$\frac{{{B_1}P}}{{{B_1}C}}=\frac{1}{2}$.
法二:设在线段B1C上存在点P,使得MP∥平面B1AD,设$\overrightarrow{{B_1}P}=λ\overrightarrow{{B_1}C}$,(0≤λ≤1),通过$\overrightarrow{MP}•\overrightarrow m=0$,
求出$\frac{{{B_1}P}}{{{B_1}C}}=\frac{1}{2}$即可.
解答  (本小题满分14分)
(本小题满分14分)
(Ⅰ)证明:由题意可知四边形ABED是平行四边形,所以AM=ME,故B1M⊥AE.
又因为AB=BE,M为AE的中点,所以BM⊥AE,
即DM⊥AE.又因为AD∥BC,AD=CE=2.
所以四边形ADCE是平行四边形.
所以AE∥CD.
故CD⊥DM.
因为平面B1AE⊥平面AECD,平面B1AE∩平面AECD=AE,B1M?平面AECD
所以B1M⊥平面AECD.B1M⊥AE.
因为CD?平面AECD,所以B1M⊥CD.
因为MD∩B1M=M,MD、B1M?平面B1MD,
所以CD⊥平面B1MD.…(5分)
(Ⅱ)解:以ME为x轴,MD为y轴,MB1为z轴建立空间直角坐标系,则$C(2,\sqrt{3},0)$,${B_1}(0,0,\sqrt{3})$,
A(-1,0,0),$D(0,\sqrt{3},0)$.
平面AB1E的法向量为$\overrightarrow{MD}$=(0,$\sqrt{3}$,0).
设平面DB1A的法向量为$\overrightarrow{m}$=(x,y,z),因为$\overrightarrow{A{B}_{1}}$=(1,0,$\sqrt{3}$),$\overrightarrow{AD}$=(1,$\sqrt{3}$,0),$\left\{\begin{array}{l}x+\sqrt{3}z=0\\ x+\sqrt{3}y=0\end{array}\right.$,
令z=1得,$\overrightarrow{m}$=(-$\sqrt{3}$,1,1).
所以cos<$\overrightarrow{m}$,$\overrightarrow{MD}$>=$\frac{\sqrt{5}}{5}$,因为二面角D-AB1-E为锐角,
所以二面角D-AB1-E的余弦值为$\frac{{\sqrt{5}}}{5}$.…(10分)
(Ⅲ) 存在点P,使得MP∥平面B1AD.…(11分)
法一:取线段B1C中点P,B1D中点Q,连结MP,PQ,AQ.
则PQ∥CD,且$PQ=\frac{1}{2}CD$.
又因为四边形AECD是平行四边形,所以$AE\underline{\underline{∥}}CD$.
因为M为AE的中点,则$AM\underline{\underline{∥}}PQ$.
所以四边形AMPQ是平行四边形,则$MP\underline{\underline{∥}}AQ$.
又因为AQ?平面AB1D,所以MP∥平面AB1D.
所以在线段B1C上存在点P,使得MP∥平面B1AD,$\frac{{{B_1}P}}{{{B_1}C}}=\frac{1}{2}$.…(14分)
法二:设在线段B1C上存在点P,使得MP∥平面B1AD,
设$\overrightarrow{{B_1}P}=λ\overrightarrow{{B_1}C}$,(0≤λ≤1),$C(2,\sqrt{3},0)$,因为$\overrightarrow{MP}=\overrightarrow{M{B_1}}+\overrightarrow{{B_1}P}$.
所以$\overrightarrow{MP}=(2λ,\sqrt{3}λ,\sqrt{3}-\sqrt{3}λ)$.
因为MP∥平面B1AD,所以$\overrightarrow{MP}•\overrightarrow m=0$,
所以$-2\sqrt{3}λ+\sqrt{3}λ+\sqrt{3}-\sqrt{3}λ=0$,解得$λ=\frac{1}{2}$,又因为MP?平面B1AD,
所以在线段B1C上存在点P,使得MP∥平面B1AD,$\frac{{{B_1}P}}{{{B_1}C}}=\frac{1}{2}$.…(14分)
点评 本题考查直线与平面垂直的判定定理的应用,二面角的平面角的求法,存在性问题的判断与证明,考查空间想象能力.

| A. | 8 | B. | 7 | C. | 4 | D. | 3 |
| A. | x=$\frac{π}{3}$ | B. | x=-$\frac{π}{6}$ | C. | x=-$\frac{π}{24}$ | D. | x=$\frac{11π}{24}$ |
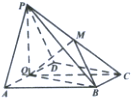 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC的中点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC的中点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$.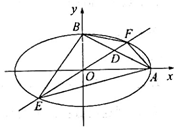 如图,已知椭圆:$\frac{{x}^{2}}{4}$+y2=1,点A,B是它的两个顶点,过原点且斜率为k的直线l与线段AB相交于点D,且与椭圆相交于E、F两点.
如图,已知椭圆:$\frac{{x}^{2}}{4}$+y2=1,点A,B是它的两个顶点,过原点且斜率为k的直线l与线段AB相交于点D,且与椭圆相交于E、F两点. 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°PA=PD=AD=2BC=2,CD=$\sqrt{3},PB=\sqrt{6}$,Q是AD的中点,M是棱PC上的点,且PM=3MC.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°PA=PD=AD=2BC=2,CD=$\sqrt{3},PB=\sqrt{6}$,Q是AD的中点,M是棱PC上的点,且PM=3MC.