题目内容
对于函数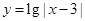 和
和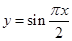
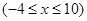 ,下列说法正确的是 .
,下列说法正确的是 .
(1)函数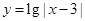 的图像关于直线
的图像关于直线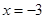 对称;
对称;
(2)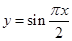
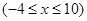 的图像关于直线
的图像关于直线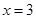 对称;
对称;
(3)两函数的图像一共有10个交点;
(4)两函数图像的所有交点的横坐标之和等于30;
(5)两函数图像的所有交点的横坐标之和等于24.
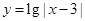 和
和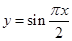
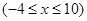 ,下列说法正确的是 .
,下列说法正确的是 .(1)函数
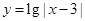 的图像关于直线
的图像关于直线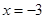 对称;
对称;(2)
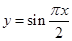
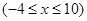 的图像关于直线
的图像关于直线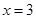 对称;
对称;(3)两函数的图像一共有10个交点;
(4)两函数图像的所有交点的横坐标之和等于30;
(5)两函数图像的所有交点的横坐标之和等于24.
(2)(3)(4);
试题分析:根据题意,由于(1)函数
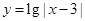 的图像关于直线
的图像关于直线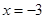 对称;不符合题意,应该是关于x=3对称才成立。
对称;不符合题意,应该是关于x=3对称才成立。(2)
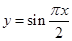
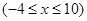 的图像关于直线
的图像关于直线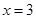 对称;将x=3代入函数值取得最值成立。
对称;将x=3代入函数值取得最值成立。(3)两函数的图像一共有10个交点;结合图像与图像的交点问题可知成立。
(4)两函数图像的所有交点的横坐标之和等于30;结合定义域
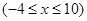 可以作图得到成立。
可以作图得到成立。(5)两函数图像的所有交点的横坐标之和等于24,由上可知不成立,故答案为(2)(3)(4)
点评:主要是考查了函数的图像与性质的综合运用,属于中档题。

练习册系列答案
相关题目
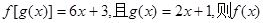 的解析式为 ( )
的解析式为 ( )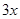
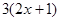
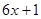
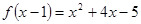 ,则
,则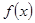 的表达式是 ___ .
的表达式是 ___ .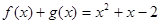 ,求f(x)和g(x)的解析式。
,求f(x)和g(x)的解析式。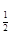 (
(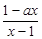 )为奇函数,a为常数.
)为奇函数,a为常数.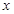 的值,不等式
的值,不等式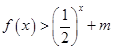 恒成立,求实数
恒成立,求实数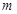 的取值范围.
的取值范围.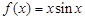 ,则
,则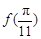 ,
,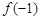 ,
,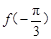 的大小关系为
的大小关系为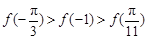
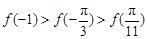
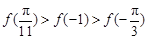
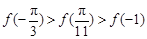
 的图象大致是
的图象大致是
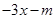
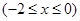 有两个不同的交点,求实数m的取值范围.
有两个不同的交点,求实数m的取值范围.