题目内容
底面是正方形的四棱锥A-BCDE中,AE⊥底面BCDE,且AE=CD=a,G、H分别是BE、ED的中点,则GH到平面ABD的距离是 .
【答案】分析:连接BD,设点E到平面ABD的距离为h,利用VA-EBD=VE-ABD求出E到平面ABD的距离,然后求出GH到平面ABD的距离.
解答: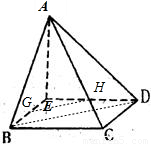 解:连接BD,设点E到平面PBD的距离为h,
解:连接BD,设点E到平面PBD的距离为h,
则由AE⊥底面BCDE,且AE=CD=a,∴△ABD是边长为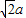 的正三角形,
的正三角形,
而由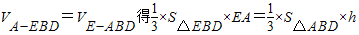 ,
,
即S△ABD×h=S△EBD×EA.
又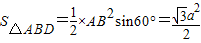 ,
,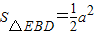 ,
,
∴
故点E到平面ABD的距离为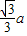 .
.
因为G、H分别是BE、ED的中点,所以GH∥BD,
GH到平面ABD的距离是点E到平面ABD的距离的一半,即 .
.
故答案为: .
.
点评:本题主要考查直线到平面的距离,以及三棱锥的体积的计算,体积的求解在最近两年高考中频繁出现,值得重视.
解答:
 解:连接BD,设点E到平面PBD的距离为h,
解:连接BD,设点E到平面PBD的距离为h,则由AE⊥底面BCDE,且AE=CD=a,∴△ABD是边长为
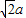 的正三角形,
的正三角形,而由
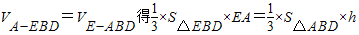 ,
,即S△ABD×h=S△EBD×EA.
又
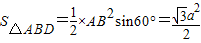 ,
,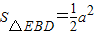 ,
,∴

故点E到平面ABD的距离为
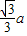 .
.因为G、H分别是BE、ED的中点,所以GH∥BD,
GH到平面ABD的距离是点E到平面ABD的距离的一半,即
 .
.故答案为:
 .
.点评:本题主要考查直线到平面的距离,以及三棱锥的体积的计算,体积的求解在最近两年高考中频繁出现,值得重视.

练习册系列答案
相关题目
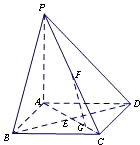 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点. 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.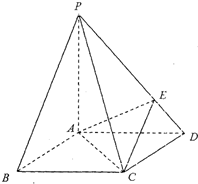 如图,在底面是正方形的四棱锥P-ABCD中,PA=AC=2,PB=PD=
如图,在底面是正方形的四棱锥P-ABCD中,PA=AC=2,PB=PD=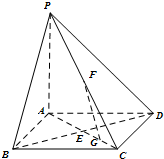 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一动点.
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一动点.