题目内容
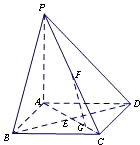 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.(Ⅰ)求证:BD⊥FG;
(Ⅱ)确定点G在线段AC上的位置,使FG∥平面PBD,并说明理由;
(Ⅲ)当二面角B-PC-D的大小为
| 2π | 3 |
分析:(Ⅰ)要证:BD⊥FG,先证BD⊥平面PAC即可.
(Ⅱ)确定点G在线段AC上的位置,使FG∥平面PBD,FG∥平面PBD内的一条直线即可.
(Ⅲ)当二面角B-PC-D的大小为
时,求PC与底面ABCD所成角的正切值.
只要作出二面角的平面角,解三角形即可求出结果.
这三个问题可以利用空间直角坐标系,解答(Ⅰ)求数量积即可.
(Ⅱ)设才点的坐标,向量共线即可解答.
(Ⅲ)利用向量数量积求解法向量,然后转化求出PC与底面ABCD所成角的正切值.
(Ⅱ)确定点G在线段AC上的位置,使FG∥平面PBD,FG∥平面PBD内的一条直线即可.
(Ⅲ)当二面角B-PC-D的大小为
| 2π |
| 3 |
只要作出二面角的平面角,解三角形即可求出结果.
这三个问题可以利用空间直角坐标系,解答(Ⅰ)求数量积即可.
(Ⅱ)设才点的坐标,向量共线即可解答.
(Ⅲ)利用向量数量积求解法向量,然后转化求出PC与底面ABCD所成角的正切值.
解答:证明:(Ⅰ)∵PA⊥面ABCD,四边形ABCD是正方形,其对角线BD,AC交于点E,
∴PA⊥BD,AC⊥BD,
∴BD⊥平面PAC,
∵FG?平面PAC,
∴BD⊥FG(5分)
解(Ⅱ):当G为EC中点,即AG=
AC时,FG∥平面PBD,(7分)
理由如下:
连接PE,由F为PC中点,G为EC中点,知FG∥PE,
而FG?平面PBD,PE?平面PBD,
故FG∥平面PBD.(9分)
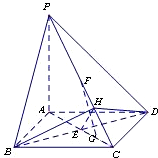 解(Ⅲ):作BH⊥PC于H,连接DH,
解(Ⅲ):作BH⊥PC于H,连接DH,
∵PA⊥面ABCD,四边形ABCD是正方形,
∴PB=PD,
又∵BC=DC,PC=PC,
∴△PCB≌△PCD,
∴DH⊥PC,且DH=BH,
∴∠BHD就是二面角B-PC-D的平面角,(11分)
即∠BHD=
,
∵PA⊥面ABCD,∴∠PCA就是PC与底面ABCD所成的角(12分)
连接EH,则EH⊥BD,∠BHE=
,EH⊥PC,
∴tan∠BHE=
=
,而BE=EC,
∴
=
,∴sin∠PCA=
=
,∴tan∠PCA=
,
∴PC与底面ABCD所成角的正切值是
(14分)
或用向量方法:
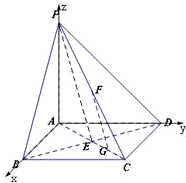
解:以A为原点,AB,AD,AP所在的直线分别为x,y,z轴建立空间直角坐标系如图所示,设正方形ABCD的边长为1,则A(0,0,0),B(1,0,0),C(1,1,0),D(0,1,0),P(0,0,a)(a>0),
E(
,
,0),F(
,
,
),G(m,m,0)(0<m<
)(2分)
(Ⅰ)
=(-1,1,0),
=(m-
,m-
,-
),
×
=-m+
+m-
+0=0,
∴BD⊥FG(5分)
(Ⅱ)要使FG∥平面PBD,只需FG∥EP,而
=(
,
,-a),由
=
可得
,
解得l=1,m=
,(7分)
∴G(
,
,0),∴
=
,
故当AG=
AC时,FG∥平面PBD(9分)
(Ⅲ)设平面PBC的一个法向量为
=(x,y,z),
则
,而
=(1,1,-a),
=(0,1,0),
∴
,取z=1,得
=(a,0,1),同理可得平面PDC的一个法向量为
=(0,a,1),
设
,
所成的角为β,则|cosβ|=|cos
|=
,即
=
,∴
=
,∴a=1(12分)
∵PA⊥面ABCD,∴∠PCA就是PC与底面ABCD所成的角,
∴tan∠PCA=
=
=
(14分)
∴PA⊥BD,AC⊥BD,
∴BD⊥平面PAC,
∵FG?平面PAC,
∴BD⊥FG(5分)
解(Ⅱ):当G为EC中点,即AG=
| 3 |
| 4 |
理由如下:
连接PE,由F为PC中点,G为EC中点,知FG∥PE,
而FG?平面PBD,PE?平面PBD,
故FG∥平面PBD.(9分)
 解(Ⅲ):作BH⊥PC于H,连接DH,
解(Ⅲ):作BH⊥PC于H,连接DH,∵PA⊥面ABCD,四边形ABCD是正方形,
∴PB=PD,
又∵BC=DC,PC=PC,
∴△PCB≌△PCD,
∴DH⊥PC,且DH=BH,
∴∠BHD就是二面角B-PC-D的平面角,(11分)
即∠BHD=
| 2π |
| 3 |
∵PA⊥面ABCD,∴∠PCA就是PC与底面ABCD所成的角(12分)
连接EH,则EH⊥BD,∠BHE=
| π |
| 3 |
∴tan∠BHE=
| BE |
| EH |
| 3 |
∴
| EC |
| EH |
| 3 |
| EH |
| EC |
| ||
| 3 |
| ||
| 2 |
∴PC与底面ABCD所成角的正切值是
| ||
| 2 |
或用向量方法:
解:以A为原点,AB,AD,AP所在的直线分别为x,y,z轴建立空间直角坐标系如图所示,设正方形ABCD的边长为1,则A(0,0,0),B(1,0,0),C(1,1,0),D(0,1,0),P(0,0,a)(a>0),
E(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| a |
| 2 |
| 2 |
(Ⅰ)
| BD |
| FG |
| 1 |
| 2 |
| 1 |
| 2 |
| a |
| 2 |
| BD |
| FG |
| 1 |
| 2 |
| 1 |
| 2 |
∴BD⊥FG(5分)
(Ⅱ)要使FG∥平面PBD,只需FG∥EP,而
| EP |
| 1 |
| 2 |
| 1 |
| 2 |
| FG |
| 1 |
| 2 |
| EP |
|

解得l=1,m=
| 3 |
| 4 |
∴G(
| 3 |
| 4 |
| 3 |
| 4 |
| AG |
| 3 |
| 4 |
| AC |
故当AG=
| 3 |
| 4 |
(Ⅲ)设平面PBC的一个法向量为
| u |
则
|
| PC |
| BC |
∴
|
| u |
| v |
设
| u |
| v |
| 2π |
| 3 |
| 1 |
| 2 |
|
| ||||
|
|
| 1 |
| 2 |
| 1 | ||||
|
| 1 |
| 2 |
∵PA⊥面ABCD,∴∠PCA就是PC与底面ABCD所成的角,
∴tan∠PCA=
| PA |
| AC |
| 1 | ||
|
| ||
| 2 |
点评:本题考查直线与平面、平面与平面的性质,空间直线的位置关系,空间直角坐标系,空间想象能力,逻辑思维能力,是难度较大题目.

练习册系列答案
相关题目
 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.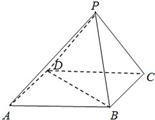 如图,在底面是正方形的四棱锥P-ABCD中,平面PCD⊥平面ABCD,PC=PD=CD=2.
如图,在底面是正方形的四棱锥P-ABCD中,平面PCD⊥平面ABCD,PC=PD=CD=2. 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点. 如图,在底面是正方形的四棱锥P-ABCD中,平面PCD⊥平面ABCD,PC=PD=CD=2.
如图,在底面是正方形的四棱锥P-ABCD中,平面PCD⊥平面ABCD,PC=PD=CD=2.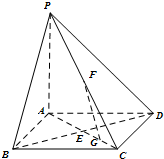 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一动点.
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一动点.