题目内容
18.在等比数列{an}中,a1>0,则“a1<a4”是“a3<a5”的( )| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 根据充分条件和必要条件的定义结合等比数列的性质进行判断即可.
解答 解:在等比数列中,若a1<a4,即a1<a1q3,
∵a1>0,∴1<q3,
即q>1,则$\frac{{a}_{5}}{{a}_{3}}={q}^{2}$>1,即a3<a5成立,
若等比数列1,-2,4,-8,16,
满足a3<a5,但a1<a4不成立,
故“a1<a4”是“a3<a5”的充分不必要条件,
故选:A
点评 本题主要考查充分条件和必要条件的判断,结合等比数列的性质是解决本题的关键.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
8.若过点(2,0)的直线l与圆C:x2+y2=1有公共点,则直线l的斜率k的取值范围是( )
| A. | [-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$] | B. | (-∞,-$\frac{\sqrt{3}}{3}$]∪[$\frac{\sqrt{3}}{3}$,+∞) | C. | $[{-\sqrt{3},\sqrt{3}}]$ | D. | $({-∞,-\sqrt{3}}]∪[{\sqrt{3},+∞})$ |
9.已知双曲线C1:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点F也是抛物线C2:y2=2px(p>0)的焦点,C1与C2的一个交点为P,若PF⊥x轴,则双曲线C1的离心率为( )
| A. | $\sqrt{2}$+1 | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{2}$-1 | D. | $\sqrt{3}$+1 |
3. 已知某几何体的三视图如图所示,其中正视图、侧视图均是由直角三角形与半圆构成,俯视图由圆与内接直角三角形构成,根据图中的数据可得此几何体体积为( )
已知某几何体的三视图如图所示,其中正视图、侧视图均是由直角三角形与半圆构成,俯视图由圆与内接直角三角形构成,根据图中的数据可得此几何体体积为( )
 已知某几何体的三视图如图所示,其中正视图、侧视图均是由直角三角形与半圆构成,俯视图由圆与内接直角三角形构成,根据图中的数据可得此几何体体积为( )
已知某几何体的三视图如图所示,其中正视图、侧视图均是由直角三角形与半圆构成,俯视图由圆与内接直角三角形构成,根据图中的数据可得此几何体体积为( )| A. | $\frac{4\sqrt{2}π}{3}$+$\frac{4}{3}$ | B. | $\frac{8\sqrt{2}π}{3}$+$\frac{4}{3}$ | C. | $\frac{4\sqrt{2}π}{3}$+2 | D. | $\frac{8\sqrt{2}π}{3}$+2 |
10.已知双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{6}$=1与抛物线y2=2px有公共焦点F,双曲线与抛物线的准线交于M、N两点,且△MNF为等边三角形,则p的值为( )
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4$\sqrt{2}$ | D. | 6 |
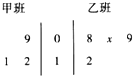 如图,茎叶图记录了某校甲班3名同学在一学年中去社会实践基地A实践的次数和乙班4名同学在同一学年中去社会实践基地B实践的次数.乙班记录中有一个数据模糊,无法确认,在图中用x表示.
如图,茎叶图记录了某校甲班3名同学在一学年中去社会实践基地A实践的次数和乙班4名同学在同一学年中去社会实践基地B实践的次数.乙班记录中有一个数据模糊,无法确认,在图中用x表示.