题目内容
若关于x的不等式
<x+a的解是x>m,试求m的最小值为
.
| 2x+1 |
| 3 |
| 2 |
| 3 |
| 2 |
分析:先作出y=
的图象,y=x+a的图象斜率为1,在曲线上方的直线部分为不等式的解集,利用图象,即可求m的最小值.
| 2x+1 |
解答: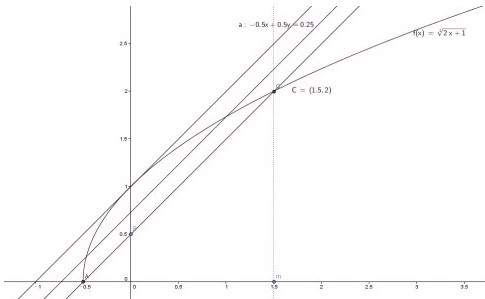 解:先作出y=
解:先作出y=
的图象,y=x+a的图象斜率为1,在曲线上方的直线部分为不等式的解集
∵解集为x>m(取不到等号)
∴只能是过A点斜率为1的直线
把A点的坐标代入y=x+a得a=0.5
再将y=x+0.5与y=
联立解得x=-0.5(舍)或1.5
即求出了交点C(1.5,2)
由数形结合可知m最小值为
故答案为
 解:先作出y=
解:先作出y=| 2x+1 |
∵解集为x>m(取不到等号)
∴只能是过A点斜率为1的直线
把A点的坐标代入y=x+a得a=0.5
再将y=x+0.5与y=
| 2x+1 |
即求出了交点C(1.5,2)
由数形结合可知m最小值为
| 3 |
| 2 |
故答案为
| 3 |
| 2 |
点评:本题的考点是不等式的综合,主要考查根式不等式的解集问题,采用数形结合是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目