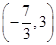题目内容
若关于x的不等式|2x+3|+|2x-1|≤a有解,则实数a的取值范围为 .
分析:由于|x+
|+|x-
|表示数轴上的x对应点到-
和
对应点的距离之和,求出|2x+3|+|2x-1|的最小值,再根据|2x+3|+|2x-1|≤a有解,求出实数a的取值范围.
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
解答:解:不等式|2x+3|+|2x-1|≤a转化为:2(|x+
|+|x-
|)≤a.
|x+
|+|x-
|表示数轴上的x对应点到-
和
对应点的距离之和,其最小值为2,
2(|x+
|+|x-
|)的最小值为4,故当a≥4时,关于x的不等式|2x+3|+|2x-1|≤a有解,
故实数a的取值范围为[4,+∞),
故答案为:[4,+∞).
| 3 |
| 2 |
| 1 |
| 2 |
|x+
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
2(|x+
| 3 |
| 2 |
| 1 |
| 2 |
故实数a的取值范围为[4,+∞),
故答案为:[4,+∞).
点评:本题主要考查绝对值的意义,绝对值不等式的解法,属于中档题.

练习册系列答案
相关题目
若关于x的不等式2-x2>|x-a|至少有一个负数解,则a的取值范围为( )
A、(-
| ||
B、(-
| ||
C、(-
| ||
D、(-
|
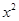 >|x-a|
至少有一个负数解,则实数a的取值范围是
.
>|x-a|
至少有一个负数解,则实数a的取值范围是
.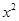 >|x-a| 至少有一个负数解,则a的取值范围为(
)
>|x-a| 至少有一个负数解,则a的取值范围为(
) B.
B.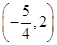 C.
C.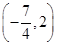 D.
D.