题目内容
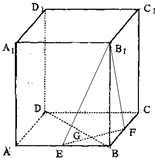 如图,正四棱柱ABCD-A1B1C1D1中,底面边长为2
如图,正四棱柱ABCD-A1B1C1D1中,底面边长为2| 2 |
(1)求证:平面EFB1⊥平面BDD1B1;
(2)求点B到平面B1EF的距离.
分析:(1)要证面EFB1⊥面BDD1B1,可先证明EF⊥平面BDD1B1,证出 EF⊥BD,EF⊥BB1即可.
(2)在平面BDD1B1中,作BH⊥B1G于为H,说明BH⊥面B1EF,BH就是点B到平面B1EF的距离,在Rt△B1BG中利用等面积法求出BH.
(2)在平面BDD1B1中,作BH⊥B1G于为H,说明BH⊥面B1EF,BH就是点B到平面B1EF的距离,在Rt△B1BG中利用等面积法求出BH.
解答:解:(1)证明:∵EF∥AC,AC⊥BD,∴EF⊥BD,根据正四棱柱的性质EF⊥BB1,BD∩BB1=B,可知EF⊥平面BDD1B1,…(3分)
又EF?面B1EF,∴面EFB1⊥面BDD1B1…(7分)
(2)可知∴面EFB1⊥面BDD1B1,在平面BDD1B1中,作BH⊥B1G于为H,∵面EFB1⊥面BDD1B1,面EFB1∩面BDD1B1=B1G
∴BH⊥面B1EF,BH就是点B到平面B1EF的距离…(10分)
在Rt△B1BG中,B1B=4,BG=1,BH⊥B1G⇒BH=
=
…(12分)
又EF?面B1EF,∴面EFB1⊥面BDD1B1…(7分)
(2)可知∴面EFB1⊥面BDD1B1,在平面BDD1B1中,作BH⊥B1G于为H,∵面EFB1⊥面BDD1B1,面EFB1∩面BDD1B1=B1G
∴BH⊥面B1EF,BH就是点B到平面B1EF的距离…(10分)
在Rt△B1BG中,B1B=4,BG=1,BH⊥B1G⇒BH=
| BG•BB1 |
| B1G |
4
| ||
| 17 |
点评:本题考查线面垂直,面面垂直的定义,性质、判定,空间距离的计算.考查了空间想象能力、计算能力,分析解决问题能力.空间问题平面化是解决空间几何体问题最主要的思想方法.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
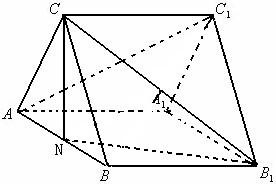 如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
 如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
