题目内容
双曲线C与椭圆![]() 有相同的焦点,直线
有相同的焦点,直线![]() 为C的一条渐近线.
为C的一条渐近线.
(1)求双曲线C的方程;
(2)过点P(0,4)的直线l交双曲线C于A、B两点,交x轴于Q点(Q点与C的顶点不重合),当![]() 时,求Q点的坐标.
时,求Q点的坐标.
解:(1)设双曲线方程为 ![]()
由椭圆![]() ,求得两焦点为(-2,0),(2,0)
,求得两焦点为(-2,0),(2,0)
∴对于双曲线C:c=2,又![]() 为双曲线C的一条渐近线,
为双曲线C的一条渐近线,
∴![]() 解得
解得 ![]() ∴双曲线C的方程为
∴双曲线C的方程为 ![]()
(2)解法一:由题意知直线l的斜率k存在且不等于零,
 设l的方程:
设l的方程:![]()
则![]()
∵![]()
∴![]()
∴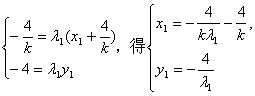
∵A(x1, y1)在双曲线C上, ∴![]()
∴![]()
∴![]()
同理有:![]()
若16-k2=0,则直线l过顶点,不合题意。
∴16-k2≠0, ∴![]() 是二次方程
是二次方程 ![]() 的两根
的两根
∴![]() ∴k2=4,此时△>0, ∴k=±2
∴k2=4,此时△>0, ∴k=±2
∴所求Q的坐标为(±2,0)
解法二:由题意知直线l的斜率k存在且不等于零。
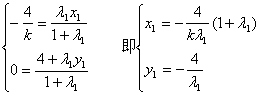
设l的方程:![]()
∵![]() ∴Q分
∴Q分![]() 的比为
的比为![]() 。由定比分点坐标式得:
。由定比分点坐标式得:
 下同解法一
下同解法一
解法三:由题意知直线l的斜率k存在且不等于零。
设l的方程:![]()
∵![]() ∴
∴![]()
∴![]()
![]()
∴![]() 即
即![]()
将![]()
∵![]() ,否则l与渐近线平行
,否则l与渐近线平行
∴ ![]()
∴![]() ∴
∴![]()
解法四:由题意知直线l的斜率k存在且不等于零,
设l的方程:![]()
∵![]() ∴
∴![]()
∴ 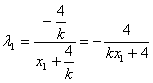
同理 ![]()
即 ![]()
又由  消去y,得
消去y,得 ![]()
当3-k2=0时,则直线l与双曲线的渐近线平行,不合题意,![]()
由韦达定理有: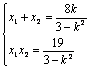
代入(*)式得k2=4,k=±2
∴所求Q的点的坐标为(±2,0)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

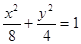 有相同的焦点,实半轴长为
有相同的焦点,实半轴长为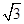 .
. 的方程;
的方程;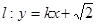 与双曲线
与双曲线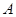 和
和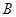 ,且
,且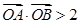
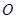 为原点),求
为原点),求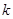 的取值范围.
的取值范围.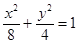 有相同的焦点,直线y=
有相同的焦点,直线y=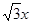 为
为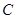 的一条渐近线.
的一条渐近线. 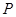 (0,4)的直线
(0,4)的直线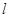 ,交双曲线
,交双曲线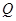 点(
点(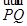 =
=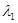
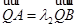 ,且
,且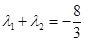 时,求
时,求