题目内容
已知关于x的方程x2-ax+ab=0,其中a,b为实数,且a≠0.(1)若
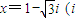 为虚数单位)是该方程的一个根,求a,b的值;
为虚数单位)是该方程的一个根,求a,b的值;(2)当该方程没有实数根时,证明:
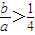 .
.
【答案】分析:(1)由已知,得另一根为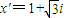 ,利用一元二次方程根与系数的关系求出a和b的值
,利用一元二次方程根与系数的关系求出a和b的值
(2)方程没有实数根,则△<0,化简后再证明.
解答:解:(1)根据一元二次方程有虚数解时,两根互为共轭虚数.由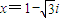 ,得另一根为
,得另一根为 ,
,
由韦达定理得x+x′=a=2,ab=x•x′= =4,b=2.----------------(6分)
=4,b=2.----------------(6分)
(2)方程没有实数根 则由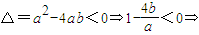
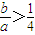 ----------(12分)
----------(12分)
点评:本题考查一元二次方程解,及根与系数的关系.若一元二次方程有虚数解,则两根互为共轭虚数,且韦达定理仍然成立.
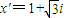 ,利用一元二次方程根与系数的关系求出a和b的值
,利用一元二次方程根与系数的关系求出a和b的值 (2)方程没有实数根,则△<0,化简后再证明.
解答:解:(1)根据一元二次方程有虚数解时,两根互为共轭虚数.由
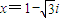 ,得另一根为
,得另一根为 ,
,由韦达定理得x+x′=a=2,ab=x•x′=
 =4,b=2.----------------(6分)
=4,b=2.----------------(6分)(2)方程没有实数根 则由
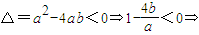
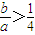 ----------(12分)
----------(12分)点评:本题考查一元二次方程解,及根与系数的关系.若一元二次方程有虚数解,则两根互为共轭虚数,且韦达定理仍然成立.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目