题目内容
已知函数f(x)=2
sinωxcosωx+2cos2ωx,(其中0<ω<1),若点(-
,1)是函数f(x)图象的一个对称中心.
(Ⅰ)试求ω的值;
(Ⅱ)当x∈[-π,π]时,先列表再作出函数f(x)在区间上的图象,并求出值域.
| 3 |
| π |
| 6 |
(Ⅰ)试求ω的值;
(Ⅱ)当x∈[-π,π]时,先列表再作出函数f(x)在区间上的图象,并求出值域.
分析:将函数f(x)解析式利用二倍角的正弦、余弦函数公式化简,再利用两角和与差的正弦函数公式化为一个角的正弦函数,
(Ⅰ)由点(-
,1)是函数f(x)图象的一个对称中心,根据正弦函数的对称性,代入得到-
+
=kπ,k∈Z,根据ω的范围,即可求出ω的值;
(Ⅱ)由第一问确定的ω的值,得到函数f(x)的解析式,列表,描点,连线,作出函数图象,由函数图象即可得到f(x)在x∈[-π,π]时的值域.
(Ⅰ)由点(-
| π |
| 6 |
| ωπ |
| 3 |
| π |
| 6 |
(Ⅱ)由第一问确定的ω的值,得到函数f(x)的解析式,列表,描点,连线,作出函数图象,由函数图象即可得到f(x)在x∈[-π,π]时的值域.
解答:解:由题设得:f(x)=
sin2ωx+cos2ωx+1=2sin(2ωx+
)+1,
(Ⅰ)∵点(-
,1)是函数f(x)图象的一个对称中心,
∴-
+
=kπ,k∈Z,
∴ω=-3k+
,
∵0<ω<1,
∴k=0,ω=
;
(Ⅱ)由(Ⅰ)知f(x)=2sin(x+
)+1,x∈[-π,π],
列表如下:
f(x)在x∈[-π,π]上的图象如图示:
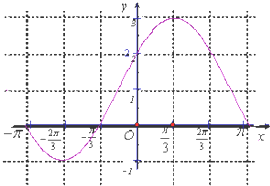
由图可知,函数在x∈[-π,π]上的值域是[-1,3].
| 3 |
| π |
| 6 |
(Ⅰ)∵点(-
| π |
| 6 |
∴-
| ωπ |
| 3 |
| π |
| 6 |
∴ω=-3k+
| 1 |
| 2 |
∵0<ω<1,
∴k=0,ω=
| 1 |
| 2 |
(Ⅱ)由(Ⅰ)知f(x)=2sin(x+
| π |
| 6 |
列表如下:
x+
|
-
|
-
|
0 |
|
π |
| ||||||||||
| x | -π | -
|
-
|
|
|
π | ||||||||||
| y | 0 | -1 | 1 | 3 | 1 | 0 |

由图可知,函数在x∈[-π,π]上的值域是[-1,3].
点评:此题考查了二倍角的正弦、余弦函数公式,两角和与差的正弦函数公式,正弦函数的对称性,以及五点法作三角函数图象,熟练掌握公式是解本题的关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目