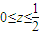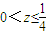题目内容
已知实数x、y、z满足x+2y+3z=1,则x2+y2+z2的最小值为______.
由柯西不等式可知:(x+2y+3z)2≤(x2+y2+z2+)(12+22+32)
故x2+y2+z2≥
,当且仅当
=
=
,
即:x2+y2+z2的最小值为
.
故答案为:
故x2+y2+z2≥
| 1 |
| 14 |
| x |
| 1 |
| y |
| 2 |
| z |
| 3 |
即:x2+y2+z2的最小值为
| 1 |
| 14 |
故答案为:
| 1 |
| 14 |

练习册系列答案
相关题目
 ,则z的取值范围是( )
,则z的取值范围是( )