题目内容
在△ABC中, =1:2:3,则
=1:2:3,则 等于( )
等于( )
 =1:2:3,则
=1:2:3,则 等于( )
等于( )A. | B. | C. | D. |
C
考点:
分析:先根据角度的比值求出各角的值进而可得其正弦值,最后根据正弦定理可得答案.
解答:解:∵在△ABC中三角比为:A:B:C=1:2:3
A=30°,B=60°,C=90°
∴sinA=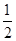 ,sinB=
,sinB=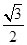 ,sinC=1
,sinC=1
根据正弦定理可知: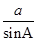 =
=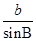 =
=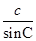
∴a:b:c=
故答案为:
点评:本题主要考查正弦定理的应用.属基础题.
分析:先根据角度的比值求出各角的值进而可得其正弦值,最后根据正弦定理可得答案.
解答:解:∵在△ABC中三角比为:A:B:C=1:2:3
A=30°,B=60°,C=90°
∴sinA=
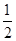 ,sinB=
,sinB=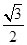 ,sinC=1
,sinC=1根据正弦定理可知:
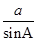 =
=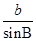 =
=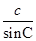
∴a:b:c=

故答案为:

点评:本题主要考查正弦定理的应用.属基础题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
 中,
中,
 的值. (2)求
的值. (2)求
 的值。
的值。 ,其中角
,其中角 是
是 的内角,
的内角,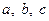 分别是角
分别是角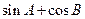 的取值范围.
的取值范围. 中,
中, 是斜边上的高线,
是斜边上的高线, 则
则 为( ).
为( ).



 ,b,c分别是三个内角A,B,C所对边,若
,b,c分别是三个内角A,B,C所对边,若 ,
, ,
, ,求△ABC的面积S.
,求△ABC的面积S.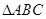 的内角A、B、C的对边分别为
的内角A、B、C的对边分别为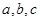 。已知
。已知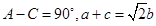 ,求C
,求C ABC中,三边a,b,c与面积s的关系式为
ABC中,三边a,b,c与面积s的关系式为 则角C为
则角C为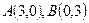 ,
,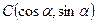 ,其中0<
,其中0<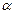 <
<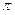 .
.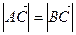 ,求角
,求角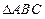 的面积为
的面积为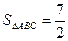 ,求
,求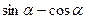 的值
的值 中
中 , 已知
, 已知  ,
,  ,
, ,则
,则 ( )
( )


