题目内容
己知函数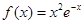 .
.
(I)求f(x)的极小值和极大值;
(II)当曲线y = f(x)的切线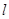 的斜率为负数时,求
的斜率为负数时,求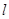 在x轴上截距的取值范围.
在x轴上截距的取值范围.
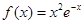 .
.(I)求f(x)的极小值和极大值;
(II)当曲线y = f(x)的切线
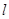 的斜率为负数时,求
的斜率为负数时,求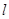 在x轴上截距的取值范围.
在x轴上截距的取值范围.(I) 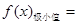 0
0 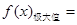
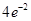 (II)
(II) 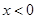 或
或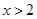
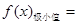 0
0 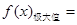
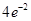 (II)
(II) 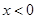 或
或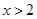
(Ⅰ)由题意知,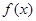 的定义域为R,因为
的定义域为R,因为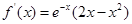 ,所以令
,所以令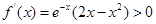 得:
得: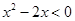 ,解得
,解得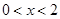 ;令
;令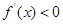 ,解得
,解得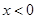 或
或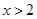 ,所以当
,所以当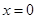 时,
时,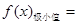 0;
0;
当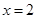 时,
时,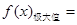
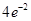 ;
;
(Ⅱ)由题意知,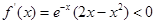 ,即
,即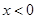 或
或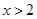 ,不难解出。
,不难解出。
本题第(Ⅰ)问,要求函数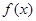 的极值,先求函数
的极值,先求函数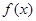 的定义域、导数、判断导数的正负,可以得出结果;第(Ⅱ)问,先由导数小于0,解得
的定义域、导数、判断导数的正负,可以得出结果;第(Ⅱ)问,先由导数小于0,解得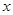 的取值范围,然后结合直线的截距式方程写出直线,即可求出。对第(Ⅰ)问,一部分同学们容易忽视定义域的求解;第(Ⅱ)问,一部分同学找不思路,所以在日常复习中,要加强导数基本题型的训练.
的取值范围,然后结合直线的截距式方程写出直线,即可求出。对第(Ⅰ)问,一部分同学们容易忽视定义域的求解;第(Ⅱ)问,一部分同学找不思路,所以在日常复习中,要加强导数基本题型的训练.
【考点定位】本小题考查利用导数研究函数的单调性、极值、最值、证明不等式等知识,综合性较强,考查函数与方程、分类讨论等数学思想,考查同学们分析问题、解决问题的能力,熟练函数与导数的基础知识以及基本题型是解答好本类题目的关键.
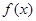 的定义域为R,因为
的定义域为R,因为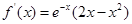 ,所以令
,所以令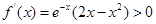 得:
得: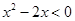 ,解得
,解得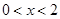 ;令
;令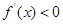 ,解得
,解得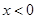 或
或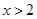 ,所以当
,所以当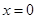 时,
时,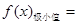 0;
0;当
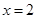 时,
时,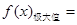
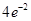 ;
;(Ⅱ)由题意知,
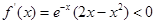 ,即
,即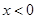 或
或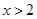 ,不难解出。
,不难解出。本题第(Ⅰ)问,要求函数
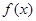 的极值,先求函数
的极值,先求函数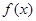 的定义域、导数、判断导数的正负,可以得出结果;第(Ⅱ)问,先由导数小于0,解得
的定义域、导数、判断导数的正负,可以得出结果;第(Ⅱ)问,先由导数小于0,解得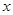 的取值范围,然后结合直线的截距式方程写出直线,即可求出。对第(Ⅰ)问,一部分同学们容易忽视定义域的求解;第(Ⅱ)问,一部分同学找不思路,所以在日常复习中,要加强导数基本题型的训练.
的取值范围,然后结合直线的截距式方程写出直线,即可求出。对第(Ⅰ)问,一部分同学们容易忽视定义域的求解;第(Ⅱ)问,一部分同学找不思路,所以在日常复习中,要加强导数基本题型的训练.【考点定位】本小题考查利用导数研究函数的单调性、极值、最值、证明不等式等知识,综合性较强,考查函数与方程、分类讨论等数学思想,考查同学们分析问题、解决问题的能力,熟练函数与导数的基础知识以及基本题型是解答好本类题目的关键.

练习册系列答案
相关题目
 (
( ).
).  时,求函数
时,求函数 的单调区间;
的单调区间; 时,
时,
 上的最小值;
上的最小值; 与
与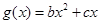 的图像都过点
的图像都过点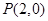 ,且它们在点
,且它们在点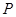 处有公共切线.
处有公共切线.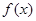 和
和 的表达式及在点
的表达式及在点 ,其中
,其中 ,求
,求 的单调区间.
的单调区间.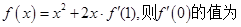 ____________。
____________。 为奇函数,且
为奇函数,且 ,则当
,则当 =( )
=( )



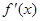 ,当
,当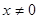 时,
时,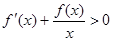 ,若
,若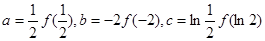 ,则下列关于a,b,c的大小关系正确的是( )
,则下列关于a,b,c的大小关系正确的是( ) ,(
,( 是互不相等的常数),则
是互不相等的常数),则 等于( )
等于( )

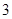

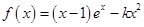 (其中
(其中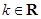 ).
).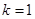 时,求函数
时,求函数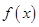 的单调区间;
的单调区间;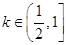 时,求函数
时,求函数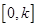 上的最大值
上的最大值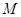 .
. 的图象在点
的图象在点 处的切线斜率为
处的切线斜率为 .
. 的值;
的值; 根的个数,证明你的结论;
根的个数,证明你的结论; ,使得曲线
,使得曲线 在该点附近的左、右的两部分分别位于曲线在该点处切线的两侧?若存在,求出点A的坐标;若不存在,说明理由.
在该点附近的左、右的两部分分别位于曲线在该点处切线的两侧?若存在,求出点A的坐标;若不存在,说明理由.