题目内容
6.已知数列{an}中,a1=1,an+1-3an=0,bn=log3an,则数列{bn}的前10项和等于( )| A. | 10 | B. | 45 | C. | 55 | D. | 39 |
分析 先求出数列{an}的通项,再利用对数的性质可知数列{bn}的通项,进而计算可得结论.
解答 解:∵a1=1,an+1-3an=0,
∴数列{an}是以1为首项、3为公比的等比数列,
∴an=${a}_{1}•{q}^{n-1}$=1•3n-1=3n-1,
∴bn=log3an=$lo{g}_{3}{3}^{n-1}$=n-1,
∴数列{bn}是以0为首项、1为公差的等差数列,
∴其前10项和为:$\frac{10(0+9)}{2}$=45,
故选:B.
点评 本题考查数列的通项及前n项和,考查运算求解能力,注意解题方法的积累,属于中档题.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
16.若某空间几何体的三视图如图所示,则该几何体的体积是( )
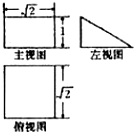

| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | 1 |
17.下列说法不正确的是( )
| A. | 若“p且q”为假,则p,q至少有一个是假命题 | |
| B. | 命题“?x∈R,x2-x-1<0”的否定是““?x∈R,x2-x-1≥0” | |
| C. | 当a<0时,幂函数y=xa在(0,+∞)上单调递减 | |
| D. | “φ=$\frac{π}{2}$”是“y=sin(2x+φ)为偶函数”的充要条件 |
14.已知函数f(x)=|sinx|,下列结论中错误的是( )
| A. | f(x)既偶函数,又是周期函数. | B. | f(x)的最大值为$\frac{\sqrt{3}}{2}$ | ||
| C. | y=f(x)的图象关于直线x=$\frac{π}{2}$对称 | D. | y=f(x)的图象关于直线x=π对称 |