题目内容
过点P(3,0)作直线l,使其被两直线2x-y-2=0和x+y+3=0所截得的线段恰好被P点所平分,试求直线l的方程.
答案:8x-y-24=0
解析:
解析:
|
解法 1:易知两直线一定相交,设所求直线l的方程为y=k(x-3),即y=kx-3k.解方程组  得 得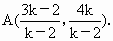
解方程组  得 得
∵线段 AB的中点为P(3,0)由中点坐标公式可得  ,解得k=8或k=0,其中k=0不合题意,舍去,由点斜式得直线l的方程为8x-y-24=0. ,解得k=8或k=0,其中k=0不合题意,舍去,由点斜式得直线l的方程为8x-y-24=0.
解法 2:设A点坐标为( ). ).
∵线段 AB的中点为P(3,0),∴可求得 B点坐标为(6-x,- ). ).
∵ A、B两点分别在直线2x-y-2=0和x+y+3=0上,可得方程组
解得 A点坐标为( ). ).
由两点式可得直线 l的方程为8x-y-24=0. |

练习册系列答案
相关题目
 +
+ =1,(a>b>0)与双曲4x2-
=1,(a>b>0)与双曲4x2- y2=1有相同的焦点,且椭C的离心e=
y2=1有相同的焦点,且椭C的离心e= ,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).
,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B). +
+ =1,(a>b>0)与双曲4x2-
=1,(a>b>0)与双曲4x2- y2=1有相同的焦点,且椭C的离心e=
y2=1有相同的焦点,且椭C的离心e= ,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).
,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B). +
+ =1,(a>b>0)与双曲4x2-
=1,(a>b>0)与双曲4x2- y2=1有相同的焦点,且椭C的离心e=
y2=1有相同的焦点,且椭C的离心e= ,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).
,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B). +
+ =1,(a>b>0)与双曲4x2-
=1,(a>b>0)与双曲4x2- y2=1有相同的焦点,且椭C的离心e=
y2=1有相同的焦点,且椭C的离心e= ,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).
,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).