题目内容
.(本小题满分14分)
如图,在边长为10的正三角形纸片ABC的边AB,AC上分别取D,E两点,使沿线段DE折叠三角形纸片后,顶点A正好落在边BC上(设为P),在这种情况下,求AD的最小值.

如图,在边长为10的正三角形纸片ABC的边AB,AC上分别取D,E两点,使沿线段DE折叠三角形纸片后,顶点A正好落在边BC上(设为P),在这种情况下,求AD的最小值.

解析:显然A,P两点关于折线DE对称,连结DP,图(2)中,设∠BAP=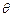 ,∠BDP=
,∠BDP= .
.
再设AD=x,所以DP=x,DB=10-x.
在△ABC中,∠APB= -∠ABP-∠BAP=
-∠ABP-∠BAP= -
-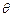 .
.
在△BDP中,由正弦定理知 =
= ,即
,即 =
= ,所以x=
,所以x= .
.
因为 ≤
≤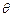 ≤
≤ ,所以
,所以 ≤
≤ -
- ≤
≤ ,所以当
,所以当 -
- =
= ,即
,即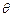 =
= 时,
时, =1.此时x取得最小值
=1.此时x取得最小值 =
= -30,且∠ADE=
-30,且∠ADE= .
.
所以AD的最小值为 -30.
-30.
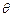 ,∠BDP=
,∠BDP= .
.再设AD=x,所以DP=x,DB=10-x.
在△ABC中,∠APB=
 -∠ABP-∠BAP=
-∠ABP-∠BAP= -
-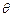 .
.在△BDP中,由正弦定理知
 =
= ,即
,即 =
= ,所以x=
,所以x= .
.因为
 ≤
≤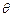 ≤
≤ ,所以
,所以 ≤
≤ -
- ≤
≤ ,所以当
,所以当 -
- =
= ,即
,即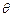 =
= 时,
时, =1.此时x取得最小值
=1.此时x取得最小值 =
= -30,且∠ADE=
-30,且∠ADE= .
.所以AD的最小值为
 -30.
-30.略

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
 ,
, 的终边上,则t的值为
的终边上,则t的值为  直线上,则2x+4y的最小值为
直线上,则2x+4y的最小值为  9平分的直线的方程是 。
9平分的直线的方程是 。