题目内容
平面直角坐标系中,点(3,t)和(2t,4)分别在顶点为原点,始边为x轴的非负半轴的角 ,
, 的终边上,则t的值为
的终边上,则t的值为
 ,
, 的终边上,则t的值为
的终边上,则t的值为 | A.±6或±1 | B.6或1 | C.6 | D.1 |
D
根据任意角的三角函数定义分别求出tanα和tan(α+45°),然后利用两角和与差的正切函数公式及特殊角的三角函数值得到一个关于t的方程,求出t的值,然后利用α和α+45°是始边为x轴的非负半轴的角,得到满足题意t的值即可.
解:由题意得tanα= ,tan(α+45°)=
,tan(α+45°)=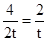
而tan(α+45°)=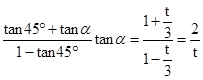 ,化简得:t2+5t-6=0即(t-1)(t+6)=0,解得t=1,t=-6
,化简得:t2+5t-6=0即(t-1)(t+6)=0,解得t=1,t=-6
因为点(3,t)和(2t,4)分别在顶点为原点,始边为x轴的非负半轴的角α,α+45°的终边上,所以t=-6舍去
则t的值为1
故选D
解:由题意得tanα=
 ,tan(α+45°)=
,tan(α+45°)=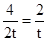
而tan(α+45°)=
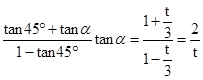 ,化简得:t2+5t-6=0即(t-1)(t+6)=0,解得t=1,t=-6
,化简得:t2+5t-6=0即(t-1)(t+6)=0,解得t=1,t=-6因为点(3,t)和(2t,4)分别在顶点为原点,始边为x轴的非负半轴的角α,α+45°的终边上,所以t=-6舍去
则t的值为1
故选D

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 经过点
经过点 ,则曲线在该点处的切线方程是 ( )
,则曲线在该点处的切线方程是 ( ) 


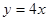 或
或
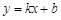 与圆
与圆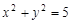 的公共点均为格点,那么这样的直线有
的公共点均为格点,那么这样的直线有 与直线
与直线 平行,则实数m= 。
平行,则实数m= 。 通过点
通过点 则有( )
则有( )




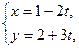 (t为参数)与直线
(t为参数)与直线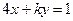 垂直,则常数k=_.
垂直,则常数k=_.