题目内容
 如图,在底面边长为
如图,在底面边长为| 2 |
(Ⅰ)求证:BD⊥平面ACC1A1;
(Ⅱ)若二面角C1-BD-C的大小为60°,求异面直线BC1与AC所成角的大小的余弦值.
分析:(Ⅰ)欲证明直线与平面垂直,可以先证明直线与直线垂直,由BD⊥CC1,BD⊥AC可得BD⊥平面ACC1A1.
(Ⅱ)先将二面角C1-BD-C的大小为60°,转化为对应的平面角的大小,根据三垂线定理可知:∠C1OC∠是二面角C1-BD-C的平面角,即∠C1OC=60°,接着就可以求解异面直线BC1与AC所成角的大小.求异面直线所成的角,可用几何法,其基本解题思路是“异面化共面,认定再计算”,即利用平移法和补形法将两条异面直线转化到同一个三角形中,结合余弦定理来求.连接A1B,由A1C1∥AC,可得∠A1C1B是BC1与AC所成的角.
(Ⅱ)先将二面角C1-BD-C的大小为60°,转化为对应的平面角的大小,根据三垂线定理可知:∠C1OC∠是二面角C1-BD-C的平面角,即∠C1OC=60°,接着就可以求解异面直线BC1与AC所成角的大小.求异面直线所成的角,可用几何法,其基本解题思路是“异面化共面,认定再计算”,即利用平移法和补形法将两条异面直线转化到同一个三角形中,结合余弦定理来求.连接A1B,由A1C1∥AC,可得∠A1C1B是BC1与AC所成的角.
解答:证明:(Ⅰ)∵ABCD-A1B1C1D1是正四棱柱,
∴CC1⊥平面ADCD,
∴BD⊥CC1
∵ABCD是正方形∴BD⊥AC
又∵AC,CC1?平面ACC1A1,且AC∩CC1=C,
∴BD⊥平面ACC1A1.
(Ⅱ)设BD与AC相交于O,连接C1O.
∵CC1⊥平面ADCD
∴BD⊥AC,∴BD⊥C1O,
∴∠C1OC∠是二面角C1-BD-C的平面角,
∴∠C1OC=60°.连接A1B.
∵A1C1∥AC,
∴∠A1C1B是BC1与AC所成的角.
∵BC=
,则
CO=1,CC1=CO•tan60°=
.A1B=BC1=
.A1C1=2.
在△A1BC1中,由余弦定理得cosA1C1B=
∴CC1⊥平面ADCD,
∴BD⊥CC1
∵ABCD是正方形∴BD⊥AC
又∵AC,CC1?平面ACC1A1,且AC∩CC1=C,
∴BD⊥平面ACC1A1.
(Ⅱ)设BD与AC相交于O,连接C1O.
∵CC1⊥平面ADCD
∴BD⊥AC,∴BD⊥C1O,
∴∠C1OC∠是二面角C1-BD-C的平面角,
∴∠C1OC=60°.连接A1B.
∵A1C1∥AC,
∴∠A1C1B是BC1与AC所成的角.
∵BC=
| 2 |
CO=1,CC1=CO•tan60°=
| 3 |
| 5 |
在△A1BC1中,由余弦定理得cosA1C1B=
| ||
| 5 |
点评:本小题主要考查空间线面关系、二面角的度量、异面直线所成的角等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.

练习册系列答案
相关题目
 ,则侧棱VA与底面所成角的大小为arcsin
,则侧棱VA与底面所成角的大小为arcsin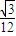 .(结果用反三角函数值表示)
.(结果用反三角函数值表示) ,则侧棱VA与底面所成角的大小为arcsin
,则侧棱VA与底面所成角的大小为arcsin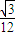 .(结果用反三角函数值表示)
.(结果用反三角函数值表示)