题目内容
如图，在底面边长为2的正三棱锥V-ABC中，E是BC的中点，若△VAE的面积是| 1 |
| 4 |
| ||
| 12 |
分析：由题意知VA与底面所成角是∠VAE，由△VAE的面积求出sin∠VAE，再用反三角函数值表示．
解答：解：在正三棱锥V-ABC中，E是BC的中点；
∴VA与底面所成角是∠VAE；
∵△VAE的面积是
，∴
=
VA•AE•sin∠VAE；
∵正三棱锥V-ABC的底面边长为2，∴AE=
，∴VAsin∠VAE=
；
即三棱锥的高为
，又顶点在底面上的投影是底面的中心，令为O，则AO=
∴VA=
=
=
∴sin∠VAE=
=
=
=
，则所求的角为arcsin
；
故选Arcsin
．
∴VA与底面所成角是∠VAE；
∵△VAE的面积是
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
∵正三棱锥V-ABC的底面边长为2，∴AE=
| 3 |
| ||
| 6 |
即三棱锥的高为
| ||
| 6 |
2
| ||
| 3 |
∴VA=
| (AO)2+(VO)2 |
(
|
|
∴sin∠VAE=
| ||||
| VA |
| ||||
|
| 1 | ||
|
| ||
| 17 |
| ||
| 17 |
故选Arcsin
| ||
| 17 |
点评：本题考查了正三棱锥的高的位置，线面角的定义及三角形的面积公式，此题是基础题．
练习册系列答案
相关题目
如图，在底面边长为
，则侧棱VA与底面所成角的大小为arcsin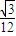
．（结果用反三角函数值表示）
，则侧棱VA与底面所成角的大小为arcsin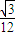
．（结果用反三角函数值表示）