题目内容
2.如图,点B、C、D都在半径为6的⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,已知∠CDB=∠OBD=30°.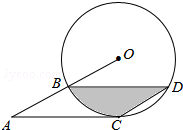
(1)求证:AC是⊙O的切线;
(2)求图中阴影部分的面积.
分析 (1)根据圆周角的性质求得∠COB=2∠CDB=60°,然后证明四边形ABDC为平行四边形,从而证得∠A=∠D=30°,根据三角形的内角和定理证得∠OCA=180°-∠A-∠COB=90°,即OC⊥AC,从而证得AC是⊙O的切线;
(2)证明△OEB≌△CED,将阴影部分面积问题转化为求扇形OBC的面积求解.
解答  (1)证明:连接OC,OC交BD于E,
(1)证明:连接OC,OC交BD于E,
∵∠CDB=30°,
∴∠COB=2∠CDB=60°,
∵∠CDB=∠OBD,
∴CD∥AB,
又∵AC∥BD,
∴四边形ABDC为平行四边形,
∴∠A=∠D=30°,
∴∠OCA=180°-∠A-∠COB=90°,即OC⊥AC,
又∵OC是⊙O的半径,
∴AC是⊙O的切线;
(2)解:∵在△OEB和△CED中,∠OBE=∠CDE,∠OEB=∠CED,BE=DE,∴△OEB≌△CED(AAS),∴S阴影=S扇形BOC.
∴S阴影=$\frac{60•π•{6}^{2}}{360}$=6π.
答:阴影部分的面积是6π.
点评 本题考查了平行四边形的判定和性质,切线的判定,平行线的性质等,连接OC构建直角三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.将120°化为弧度为( )
| A. | $-\frac{2π}{3}$ | B. | $-\frac{5π}{6}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
17.已知正项等比数列{an}满足:a7=a6+2a5,若存在两项am,an使得$\sqrt{{a_m}{a_n}}=32{a_1}$,则$\frac{1}{m}$+$\frac{4}{n}$的最小值为( )
| A. | $\frac{2}{3}$ | B. | $\frac{5}{3}$ | C. | $\frac{5}{6}$ | D. | $\frac{3}{4}$ |
7.若偶函数f(x)在(-∞,-1]上是减函数,则( )
| A. | $f(π)<f(-\frac{3}{2})<f(1)$ | B. | $f(π)<f(1)<f(-\frac{3}{2})$ | C. | $f(-\frac{3}{2})<f(1)<f(π)$ | D. | $f(1)<f(-\frac{3}{2})<f(π)$ |
14.已知$\overrightarrow{a}$=(2,0,2),$\overrightarrow{b}$=(-1,-1,0),则错误的是( )
| A. | $\overrightarrow{a}$⊥$\overrightarrow{b}$ | B. | <$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{2π}{3}$ | ||
| C. | $\overrightarrow{a}$在$\overrightarrow{b}$上的射影为-$\sqrt{2}$ | D. | $\overrightarrow{b}$在$\overrightarrow{a}$上的射影为-$\frac{\sqrt{2}}{2}$ |
11.已知定义在R上函数f(x)部分自变量与函数值对应关系如表,若f(x)为偶函数,且在[0,+∞)上为增函数,不等式1<f(x-1)<2的解集是( )
| x | 0 | 2 | 3 | 4 |
| f(x) | -1 | 1 | 2 | 3 |
| A. | (-2,-1) | B. | (3,4) | C. | (-2,-1)∪(3,4) | D. | (-2,4) |
12.在△ABC中,三角A,B,C满足关系式:sin2A+sin2B=sin2C+sinAsinB,G是△ABC垂心,且满足$\overrightarrow{CG}$•$\overrightarrow{CA}$=6,则△ABC的面积S△ABC=( )
| A. | 3 | B. | 4 | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
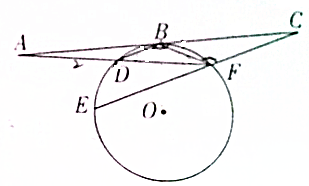 已知直线AC与⊙O相切于点B,AD交⊙O于F、D两点,CF交⊙O于E、F,BD∥CE,AB=BC,AD=2,BD=1
已知直线AC与⊙O相切于点B,AD交⊙O于F、D两点,CF交⊙O于E、F,BD∥CE,AB=BC,AD=2,BD=1