Question

（本小题满分12分）

已知F₁、F₂分别是双曲线x²-y²＝1的两个焦点，O为坐标原点，圆O是以F₁F₂为直径的圆，直线l：y＝kx+b  (b>0)与圆O相切，并与双曲线相交于A、B两点.

（Ⅰ）根据条件求出b和k满足的关系式；

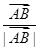（Ⅱ）向量在向量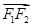方向的投影是p，当(×)p²＝1时，求直线l的方程；

（Ⅲ）当(×)p²=m且满足2≤m≤4时，求DAOB面积的取值范围.

 

Answer 1

【答案】

 

（1）b²=2(k²+1)  (k¹±1,b>0)

（2）y=±x+

（3）[3] 

【解析】解：（Ⅰ）b和k满足的关系式为b²=2(k²+1)  (k¹±1,b>0) …………3分

（Ⅱ）设A(x₁,y₁) B(x₂,y₂)，则由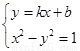消去y

得(k²-1)x²+2kbx+b²+1=0，其中k²¹1        …………4分

∴×=x₁x₂+y₁y₂=(1+k²)x₁x₂+kb(x₁+x₂)+b²

= + + 2(k²+1)

由于向量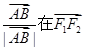方向上的投影是p

∴p²=cos²<,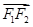>=               …………6分

∴(×)×p²= + +2=1Þk=±

∵b²= 2(k²+1)  (k¹±1,b>0)， 故b= ，经检验适合D＞0

∴直线l的方程为y=±x+               …………8分

（Ⅲ）类似于（Ⅱ）可得+ +2=m

∴k²=1+ ， b²=4+ 根据弦长公式

得  …………10分

则S_DAOB= |AB|×=

而mÎ[2,4]，∴DAOB的面积的取值范围是[3]  …………12分