题目内容
已知平面上有三点A(1,1),B(-2,4),C(-1,2),P在直线AB上,使|
|=
|
|,连接PC,Q是PC的中点,则点Q的坐标是( )
| AP |
| 1 |
| 3 |
| AB |
A、(-
| ||||
B、(
| ||||
C、(-
| ||||
D、(-
|
分析:由A和B的坐标表示出直线AB的方程,根据P在直线AB上,设出P的坐标为(e,-e+2),进而表示出
和
,根据已知的|
|=
|
|,列出关于e的方程,求出方程的解得到e的值,确定出P的坐标,然后由C和P的坐标,根据中点坐标公式即可求出Q的坐标.
| AP |
| AB |
| AP |
| 1 |
| 3 |
| AB |
解答:解:由A(1,1),B(-2,4),
得到直线AB的方程为:y-1=
(x-1),即y=-x+2,
设P(e,-e+2),
所以
=(e-1,-e+1),
=(-3,3),又|
|=
|
|,
所以
=
,即2e(e-2)=0,
解得:e=0或e=2,
则P的坐标为(0,2)或(2,0),又C(-1,2),
所以Q坐标为(-
,2)或(
,1).
故选C
得到直线AB的方程为:y-1=
| 1-4 |
| 1-(-2) |
设P(e,-e+2),
所以
| AP |
| AB |
| AP |
| 1 |
| 3 |
| AB |
所以
| (e-1)2+(-e+1)2 |
| 1 |
| 3 |
| (-3)2+32 |
解得:e=0或e=2,
则P的坐标为(0,2)或(2,0),又C(-1,2),
所以Q坐标为(-
| 1 |
| 2 |
| 1 |
| 2 |
故选C
点评:此题考查了平面向量模的计算,中点坐标公式,以及直线的两点式方程,根据A和B的坐标表示出直线AB的方程,进而设出P点坐标,根据题意列出方程,确定出P的坐标是本题的突破点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
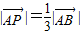 ,连接PC,Q是PC的中点,则点Q的坐标是( )
,连接PC,Q是PC的中点,则点Q的坐标是( )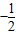 ,2)
,2) ,1)
,1)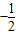 ,2)或(
,2)或( ,1)
,1)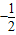 ,2)或(-1,2)
,2)或(-1,2)