题目内容
【题目】已知椭圆:![]() 的右焦点与抛物线
的右焦点与抛物线![]() 的焦点重合,曲线
的焦点重合,曲线![]() 与
与![]() 相交于点
相交于点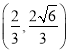 .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过右焦点![]() 的直线
的直线![]() (与
(与![]() 轴不重合)与椭圆
轴不重合)与椭圆![]() 交于
交于![]() ,
,![]() 两点,线段
两点,线段![]() 的中点
的中点![]() ,连接
,连接![]() 并延长交椭圆
并延长交椭圆![]() 于
于![]() 点(
点(![]() 为坐标原点),求四边形
为坐标原点),求四边形![]() 面积
面积![]() 的最小值.
的最小值.
【答案】(1)![]() (2)最小值为3.
(2)最小值为3.
【解析】
(1)将点带入抛物线方程,可求得![]() 的值,进而得焦点坐标;将点代入椭圆方程,并结合椭圆中
的值,进而得焦点坐标;将点代入椭圆方程,并结合椭圆中![]() 的等量关系,解方程组求得
的等量关系,解方程组求得![]() ,即可得椭圆
,即可得椭圆![]() 的方程;
的方程;
(2)方法一:设![]() ,
,![]() ,
,![]() ,直线
,直线![]() 的方程为
的方程为![]() ,联立直线与椭圆方程,由韦达定理表示出
,联立直线与椭圆方程,由韦达定理表示出![]()
![]() ,进而由弦长公式表示出弦长
,进而由弦长公式表示出弦长![]() ;由中点坐标公式表示出
;由中点坐标公式表示出![]() 的坐标,进而可表示出直线
的坐标,进而可表示出直线![]() 的方程,代入椭圆后求得
的方程,代入椭圆后求得![]() 点坐标,由点到直线距离公式求得
点坐标,由点到直线距离公式求得![]() 到
到![]() 的距离
的距离![]() 和
和![]() 到
到![]() 的距离
的距离![]() ,即可表示出四边形
,即可表示出四边形![]() 面积
面积![]() ,即可确定面积的最小值;方法二:当直线
,即可确定面积的最小值;方法二:当直线![]() 斜率不存在时,易得四边形
斜率不存在时,易得四边形![]() 面积,当斜率存在时,设
面积,当斜率存在时,设![]() ,
,![]() ,直线
,直线![]() 的方程为
的方程为![]() ,联立直线与椭圆方程,求得
,联立直线与椭圆方程,求得![]() 点坐标,同上即可.
点坐标,同上即可.
(1)![]() 点
点![]() 在
在![]() 上,
上,
![]() ,
,
![]() ,
,
![]() 椭圆
椭圆![]() 的右焦点为
的右焦点为![]() ,
,
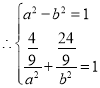 ,解得
,解得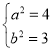 ,
,
![]() 椭圆
椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)解法一:设![]() ,
,![]() ,
,![]() ,
,
设直线AC的方程为![]() ,与椭圆方程联立得
,与椭圆方程联立得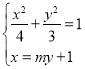 ,
,
整理得![]() .
.
由韦达定理得![]() ,
,![]() ,
,
由弦长公式可得![]()
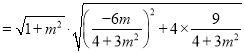
![]() ,
,
由中点坐标公式可知![]() ,
,![]() ,
,
![]() ,
,
直线OG的方程为![]() ,代入
,代入![]() ,
,
整理得![]() ,
,
![]() 取点
取点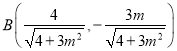 ,
,
B到直线AC的距离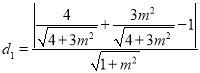
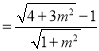 ,
,
O到直线AC的距离![]() ,
,
![]()
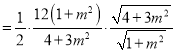
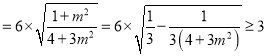 ,当且仅当
,当且仅当![]() 时取得最小值.
时取得最小值.
综上所述,四边形OABC的面积最小值是3.
解法二:①当斜率不存在时,直线AC的方程为![]() ,
,
此时![]() ;
;
②当直线AC斜率存在时,设为k,
![]() ,
,![]() ,
,
AC的方程为![]() ,
,
与椭圆方程联立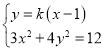 ,
,
得![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
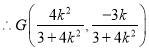 .
.
![]() 的方程为
的方程为![]() ,
,
联立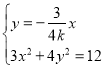 ,得
,得![]() ,
,
不妨设![]() ,
,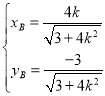 ,
,
B到直线AC的距离为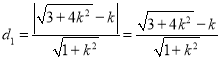 ,
,
O到直线AC的距离为![]() ,
,
由弦长公式得![]()
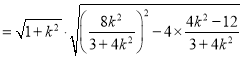
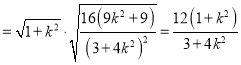 ,
,
![]()
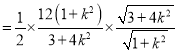
![]()
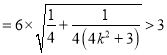 .
.
综上所述,当直线AC垂直于x轴时,![]() 面积取得最小值为3.
面积取得最小值为3.

【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 分别为内角
分别为内角![]() ,
,![]() ,
,![]() 的对边,且满
的对边,且满![]() .
.
(1)求![]() 的大小;
的大小;
(2)再在①![]() ,②
,②![]() ,③
,③![]() 这三个条件中,选出两个使
这三个条件中,选出两个使![]() 唯一确定的条件补充在下面的问题中,并解答问题.若________,________,求
唯一确定的条件补充在下面的问题中,并解答问题.若________,________,求![]() 的面积.
的面积.
【题目】自湖北武汉爆发新型冠状病毒肺炎疫情以来,各地医疗物资缺乏,各生产企业纷纷加班加点生产,某企业准备购买三台口罩生产设备,型号分别为A,B,C,已知这三台设备均使用同一种易耗品,提供设备的商家规定:可以在购买设备的同时购买该易耗品,每件易耗品的价格为100元;也可以在设备使用过程中,随时单独购买易耗品,每件易耗品的价格为200元.为了决策在购买设备时应同时购买的易耗品的件数,该单位调查了这三种型号的设备各60台,调查每台设备在一个月中使用的易耗品的件数,并得到统计表如下所示.
每台设备一个月中使用的易耗品的件数 | 6 | 7 | 8 | |
频数 | 型号A | 30 | 30 | 0 |
型号B | 20 | 30 | 10 | |
型号C | 0 | 45 | 15 | |
将调查的每种型号的设备的频率视为概率,各台设备在易耗品的使用上相互独立.
(1)求该单位一个月中A,B,C三台设备使用的易耗品总数超过21件(不包括21件)的概率;
(2)以该单位一个月购买易耗品所需总费用的期望值为决策依据,该单位在购买设备时应同时购买20件还是21件易耗品?
【题目】《中央广播电视总台2019主持人大赛》是中央人民广播电视总台成立后推出的第一个电视大赛,由撒贝宁担任主持人,康辉、董卿担任点评嘉宾,敬一丹、鲁健、朱迅、俞虹、李洪岩等17位担任专业评审.从2019年10月26日起,每周六20:00在中央电视台综合频道播出.某传媒大学为了解大学生对主持人大赛的关注情况,分别在大一和大二两个年级各随机抽取了100名大学生进行调查.下图是根据调查结果绘制的学生场均关注比赛的时间频率分布直方图和频数分布表,并将场均关注比赛的时间不低于80分钟的学生称为“赛迷”.
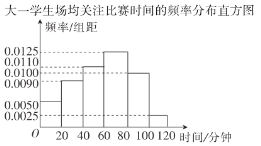
大二学生场均关注比赛时间的频数分布表
时间分组 | 频数 |
| 12 |
| 20 |
| 24 |
| 22 |
| 16 |
| 6 |
(1)将频率视为概率,估计哪个年级的大学生是“赛迷”的概率大,请说明理由;
(2)已知抽到的100名大一学生中有男生50名,其中10名为“赛迷”试完成下面的![]() 列联表,并据此判断是否有
列联表,并据此判断是否有![]() 的把握认为“赛迷”与性别有关.
的把握认为“赛迷”与性别有关.
非“赛迷” | “赛迷” | 合计 | |
男 | |||
女 | |||
合计 |
附: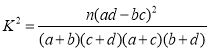 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |