题目内容
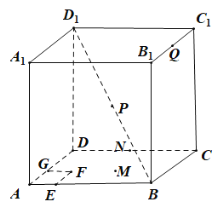
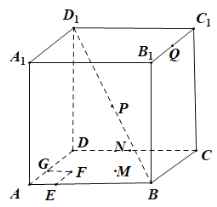
【题目】如图所示,在棱长为4的正方体![]() 中,点M是正方体表面上一动点,则下列说法正确的个数为( )
中,点M是正方体表面上一动点,则下列说法正确的个数为( )
①若点M在平面ABCD内运动时总满足![]() ,则点M在平面ABCD内的轨迹是圆的一部分;
,则点M在平面ABCD内的轨迹是圆的一部分;
②在平面ABCD内作边长为1的小正方形EFGA,点M满足在平面ABCD内运动,且到平面![]() 的距离等于到点F的距离,则M在平面ABCD内的轨迹是抛物线的一部分;
的距离等于到点F的距离,则M在平面ABCD内的轨迹是抛物线的一部分;
③已知点N是棱CD的中点,若点M在平面ABCD内运动,且![]() 平面
平面![]() ,则点M在平面
,则点M在平面![]() 内的轨迹是线段;
内的轨迹是线段;
④已知点P、Q分别是![]() ,
,![]() 的中点,点M为正方体表面上一点,若MP与CQ垂直,则点M所构成的轨迹的周长为
的中点,点M为正方体表面上一点,若MP与CQ垂直,则点M所构成的轨迹的周长为![]() .
.
A.1B.2C.3D.4
【答案】D
【解析】
对于①,结合圆锥的性质,可判断其正确;对于②,结合抛物线的定义,可知其正确;对于③,取AB的中点I,BC的中点O,易证平面![]() 平面
平面![]() ,可知当M在线段IO上时,满足题意;对于④,只需过点P作直线CQ的垂面即可,垂面与正方体表面的交线即为动点M的轨迹,求出周长,即可判断④正确.
,可知当M在线段IO上时,满足题意;对于④,只需过点P作直线CQ的垂面即可,垂面与正方体表面的交线即为动点M的轨迹,求出周长,即可判断④正确.
对于①,因为满足条件的动点M是以![]() 为轴线,以
为轴线,以![]() 为母线的圆锥与平面ABCD的交线,即圆的一部分,故①是正确的;
为母线的圆锥与平面ABCD的交线,即圆的一部分,故①是正确的;
对于②,依题意知点M到点F的距离与到直线AB的距离相等,所以M的轨迹是以F为焦点,AB为准线的抛物线,故②是正确的;
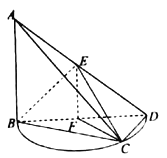
对于③,如图(1),取AB的中点I,BC的中点O,显然![]() ,
,![]() ,从而可以证明平面
,从而可以证明平面![]() 平面
平面![]() ,当M在线段IO上时,均有
,当M在线段IO上时,均有![]() 平面
平面![]() ,即动点M的轨迹是线段IO,故③是正确的;
,即动点M的轨迹是线段IO,故③是正确的;
对于④,如图(2),依题意,只需过点P作直线CQ的垂面即可,垂面与正方体表面的交线即为动点M的轨迹.分别取![]() ,
,![]() 的中点R,S,由
的中点R,S,由![]() ,知
,知![]() ,易知
,易知![]() ,又
,又![]() ,
,![]() ,所以
,所以![]() 平面ABRS,过P作平面ABRS的平行平面
平面ABRS,过P作平面ABRS的平行平面![]() ,点M的轨迹为四边形
,点M的轨迹为四边形![]() ,其周长与四边形ABRS的周长相等,所以点M所构成的轨迹的周长为
,其周长与四边形ABRS的周长相等,所以点M所构成的轨迹的周长为![]() ,故④是正确的.
,故④是正确的.
因此说法正确的有4个.
故选:D.



 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案