题目内容
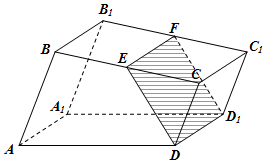
（本小题满分12分） 如图，已知直四棱柱
的底面是直角梯形，
，
，
，
分别是棱
，
上的动点，且
，
，
．
（Ⅰ）证明：无论点怎样运动，四边形
都为矩形；
（Ⅱ）当
时，求几何体
的体积。
解析：（Ⅰ）在直四棱柱
中，
，
∵
，∴
， ---------------------------------------2分
又∵平面
平面
，
平面
平面
，
平面
平面
，
∴
，∴四边形
为平行四边形，---------------------------------------4分
∵侧棱
底面
，又
平面内，
∴
，∴四边形为矩形； -----------------------------5分
（Ⅱ）证明：连结
，∵四棱柱为直四棱柱，
∴侧棱底面，又
平面内，
∴
， --------------------------------6分
在
中，
，
，则
； -----------------------------------7分
在
中，
，
，则
； -------------------------------8分
在直角梯形中，
；
∴
，即
，
又∵
，∴
平面； --------------------------10分
由（Ⅰ）可知，四边形为矩形，且，
，
∴矩形的面积为
，
∴几何体
的体积为
．-----------------------------12分
练习册系列答案
应用题作业本系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
