题目内容

12、过圆x2+y2=4外一点P（2，4）作圆的切线，切点为A、B，则△APB的外接圆方程为（x-1）2+（y-2）2=
5
．
分析：求解三角形外接圆方程，抓住P、A、O、B四点共圆，PO为直径，r很快得到．
解答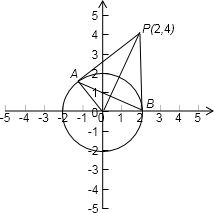：解：∵P、A、O、B四点共圆
∴易知三角形外接圆是以由PO为直径的圆
∵PO的中点为Q（1，2），故圆方程为
（x-1）2+（y-2）2=5，
故答案为（x-1）2+（y-2）2=5．
点评：本题考查了三角形外接圆方程的求解
练习册系列答案
相关题目
过圆x2+y2=4外一点P（4，2）作圆的两条切线，切点分别为A，B，则△ABP的外接圆方程是（　　）
A、（x-4）2+（y-2）2=1B、x2+（y-2）2=4C、（x+2）2+（y+1）2=5D、（x-2）2+（y-1）2=5
过圆x2+y2=4外一点P（2，1）引圆的切线，则切线的方程为
x=2或3x+4y-10=0
x=2或3x+4y-10=0
．
过圆x2+y2=4外的一点A（4，0）作圆的割线，则割线被圆截得的弦的中点的轨迹方程为
（x-2）2+y2=4（已知圆内部分）
（x-2）2+y2=4（已知圆内部分）
．
过圆x2+y2=4外一点P(-4，-2)作圆的两条切线，切点为A、B，则△ABP的外接圆的方程为(    )

A.(x-4)2+(y-2)2=1                            B.(x+2)2+(y+1)2=5

C.x2+(y-2)2=4                               D.(x-2)2+(y-1)2=5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网