题目内容
 10、如图,在杨辉三角形中,斜线l的上方从1按箭头所示方向可以构成一个“锯齿形”的数列:1,3,3,4,6,5,10,…,记此数列的前n项之和为Sn,则S21的值为( )
10、如图,在杨辉三角形中,斜线l的上方从1按箭头所示方向可以构成一个“锯齿形”的数列:1,3,3,4,6,5,10,…,记此数列的前n项之和为Sn,则S21的值为( )分析:先求通项公式a(n),在杨辉三角形中,观察数列特点,分为两类求解,n为偶数时,较易,n为奇数时,利用二项式的系数,求和也分为奇数和偶数来求,都用到等差数列的前n项和公式进行求解,奇数时还用到偶数的平方和公式.
解答:解:从杨辉三角形的生成过程,可以得到你的这个数列的通项公式a(n).
n为偶数时,a(n)=(n+4)/2,
n为奇数时,1=c20=C22,3=C31=C32,6=C42,10=C53=C52,…
a(n)=C(n+3)/22=(n+3)(n+1)/8.
然后求前21项和,偶数项和为75,
奇数项和为[(22+42+62+…+222)+2(2+4+6…+22)]/8
=[(22×4×23)+11×24]/8=286,
最后S(21)=361
故选D.
n为偶数时,a(n)=(n+4)/2,
n为奇数时,1=c20=C22,3=C31=C32,6=C42,10=C53=C52,…
a(n)=C(n+3)/22=(n+3)(n+1)/8.
然后求前21项和,偶数项和为75,
奇数项和为[(22+42+62+…+222)+2(2+4+6…+22)]/8
=[(22×4×23)+11×24]/8=286,
最后S(21)=361
故选D.
点评:本题是规律的归纳题,解决本题的关键是读懂题意,理清题意归纳出a(n)的通项公式,本题考查等差数列的前n项和公式,偶数和的公式为
22+42+62+…+(2n)2=2n(n+1)(2n+1)/3
22+42+62+…+(2n)2=2n(n+1)(2n+1)/3

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
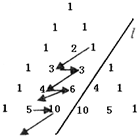 如图,在杨辉三角形中,斜线l的上方,从1开始箭头所示的数组成一个锯齿形数列:1,3,3,4,6,5,10,…,记其前n项和为Sn,则S19等于( )
如图,在杨辉三角形中,斜线l的上方,从1开始箭头所示的数组成一个锯齿形数列:1,3,3,4,6,5,10,…,记其前n项和为Sn,则S19等于( )| A、129 | B、172 | C、228 | D、283 |
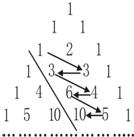 如图,在杨辉三角形中,斜线l的上方从1按箭头方向可以构成一个“锯齿形”的数列{an}:1,3,3,4,6,5,10,…,记其前n项和为Sn,则S19的值为
如图,在杨辉三角形中,斜线l的上方从1按箭头方向可以构成一个“锯齿形”的数列{an}:1,3,3,4,6,5,10,…,记其前n项和为Sn,则S19的值为
 的上方,从1开始箭头所示的数组成一个锯齿形数列:1,3,3,4,6,5,10,…,记其前n项和为Sn,则S19等于 ( )
的上方,从1开始箭头所示的数组成一个锯齿形数列:1,3,3,4,6,5,10,…,记其前n项和为Sn,则S19等于 ( )
