题目内容
如图,过曲线 :
: 上一点
上一点 作曲线
作曲线 的切线
的切线 交
交 轴于点
轴于点 ,又过
,又过 作
作
 轴的垂线交曲线
轴的垂线交曲线 于点
于点 ,然后再过
,然后再过 作曲线
作曲线 的切线
的切线 交
交 轴于点
轴于点 ,又过
,又过 作
作 轴的垂线交曲线
轴的垂线交曲线 于点
于点 ,
, ,以此类推,过点
,以此类推,过点 的切线
的切线 与
与 轴相交于点
轴相交于点 ,再过点
,再过点 作
作 轴的垂线交曲线
轴的垂线交曲线 于点
于点 (
( N
N ).
).

(1) 求 、
、 及数列
及数列 的通项公式;
的通项公式;
(2) 设曲线 与切线
与切线 及直线
及直线 所围成的图形面积为
所围成的图形面积为 ,求
,求 的表达式;
的表达式;
(3) 在满足(2)的条件下, 若数列 的前
的前 项和为
项和为 ,求证:
,求证: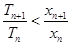
 N
N .
.
【答案】
(1) 解: 由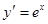 ,设直线
,设直线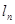 的斜率为
的斜率为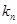 ,则
,则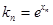 .
.
∴直线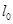 的方程为
的方程为 .令
.令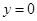 ,得
,得 , ……2分
, ……2分
∴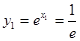 ,
∴
,
∴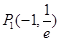 .
.
∴ .
.
∴直线 的方程为
的方程为 .令
.令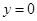 ,得
,得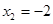 . ……4分
. ……4分
一般地,直线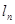 的方程为
的方程为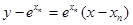 ,
,
由于点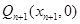 在直线
在直线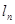 上,
上,
∴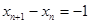 .
.
∴数列 是首项为
是首项为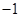 ,公差为
,公差为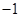 的等差数列.
的等差数列.
∴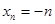 .
……6分
.
……6分
(2)解: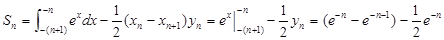

 .
……8分
.
……8分
(3)证明: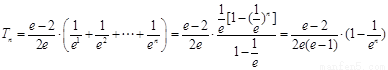 .…10分
.…10分
∴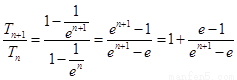 ,
,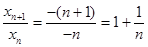 .
.
要证明 ,只要证明
,只要证明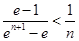 ,即只要证明
,即只要证明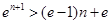 。 11分
。 11分
证法1:(数学归纳法)
① 当 时,显然
时,显然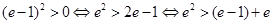 成立;
成立;
② 假设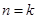 时,
时, 成立,
成立,
则当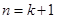 时,
时, ,
,
而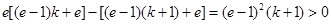 .
.
∴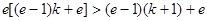 .
.
∴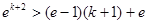 .
.
这说明,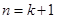 时,不等式也成立.
时,不等式也成立.
由①②知不等式 对一切
对一切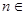 N
N 都成立. ……14分
都成立. ……14分
证法2: 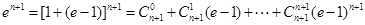
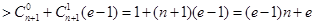 .
.
∴不等式 对一切
对一切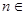 N
N 都成立. ……14分
都成立. ……14分
证法3:令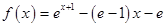 ,
,
则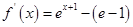 ,
,
当 时,
时, 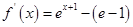
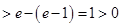 ,
,
∴函数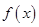 在
在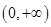 上单调递增.
上单调递增.
∴当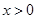 时,
时, 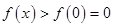 .
.
∵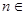 N
N ,
,
∴ , 即
, 即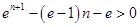 .
.
∴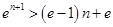 .
.
∴不等式 对一切
对一切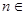 N
N 都成立.
都成立.
【解析】略

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
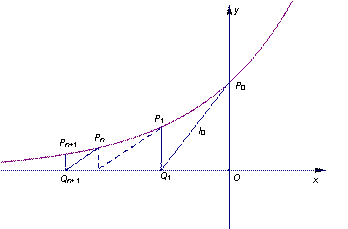
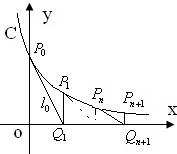 如图,过曲线C:y=e-x上一点P0(0,1)做曲线C的切线l0交x轴于Q1(x1,0)点,又过Q1做x轴的垂线交曲线C于P1(x1,y1)点,然后再过P1(x1,y1)做曲线C的切线l1交x轴于Q2(x2,0),又过Q2做x轴的垂线交曲线C于P2(x2,y2),…,以此类推,过点Pn的切线ln与x轴相交于点Qn+1(xn+1,0),再过点Qn+1做x轴的垂线交曲线C于点Pn+1(xn+1,yn+1)(n=1,2,3,…).
如图,过曲线C:y=e-x上一点P0(0,1)做曲线C的切线l0交x轴于Q1(x1,0)点,又过Q1做x轴的垂线交曲线C于P1(x1,y1)点,然后再过P1(x1,y1)做曲线C的切线l1交x轴于Q2(x2,0),又过Q2做x轴的垂线交曲线C于P2(x2,y2),…,以此类推,过点Pn的切线ln与x轴相交于点Qn+1(xn+1,0),再过点Qn+1做x轴的垂线交曲线C于点Pn+1(xn+1,yn+1)(n=1,2,3,…). :
: 上一点
上一点 作曲线
作曲线 交
交 轴于点
轴于点 ,又过
,又过 作
作  ,然后再过
,然后再过 交
交 ,又过
,又过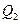 作
作 ,
, ,以此类推,过点
,以此类推,过点 的切线
的切线 与
与 ,再过点
,再过点 作
作 (
( N
N ).
).
 、
、 及数列
及数列 的通项公式;
的通项公式;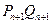 所围成的图形面积为
所围成的图形面积为 ,求
,求 的前
的前 项和为
项和为 ,求证:
,求证:
 N
N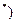 .
. (3) 在满足(2)的条件下, 若数列
(3) 在满足(2)的条件下, 若数列 (n∈N+).
(n∈N+).