题目内容
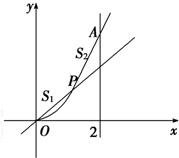 如图,设点P从原点沿曲线y=x2向点A(2,4)移动,记直线OP、曲线y=x2及直线x=2所围成的面积分别记为S1,S2,若S1=S2,求点P的坐标.
如图,设点P从原点沿曲线y=x2向点A(2,4)移动,记直线OP、曲线y=x2及直线x=2所围成的面积分别记为S1,S2,若S1=S2,求点P的坐标.
分析:本题考查的定积分的简单应用,先设直线OP的方程为y=kx,P点的坐标为(x,y),利用定积分的几何意义分别求出面积S1,S2,再利用:“S1=S2,”列出方程解之即得正确的答案.
解答:解:设直线OP的方程为y=kx,P点的坐标为(x,y),
则∫0x(kx-x2)dx=∫x2(x2-kx)dx,
即(
kx2-
x3)|0x=(
x3-
kx2)|x2,
解得
kx2-
x3=
-2k-(
x3-
kx2),
解得k=
,即直线OP的方程为y=
x,
所以点P的坐标为(
,
).
则∫0x(kx-x2)dx=∫x2(x2-kx)dx,
即(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
解得
| 1 |
| 2 |
| 1 |
| 3 |
| 8 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
解得k=
| 4 |
| 3 |
| 4 |
| 3 |
所以点P的坐标为(
| 4 |
| 3 |
| 16 |
| 9 |
点评:解答定积分的计算题,关键是熟练掌握定积分的相关性质:①∫ab1dx=b-a②∫abkf(x)dx=k∫abf(x)dx③∫abf(x)±g(x)dx=∫abf(x)dx±∫abg(x)dx.定积分就是求函数F(X)在区间(a,b)中图线下包围 的面积.即 y=0 x=a x=b y=F(X)所包围的面积.

练习册系列答案
相关题目
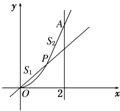 如图,设点P从原点沿曲线y=x2向点A(2,4)移动,记直线OP、曲线y=x2及直线x=2所围成的面积分别记为S1,S2,若S1=S2,则点P的坐标为
如图,设点P从原点沿曲线y=x2向点A(2,4)移动,记直线OP、曲线y=x2及直线x=2所围成的面积分别记为S1,S2,若S1=S2,则点P的坐标为
