题目内容
(本小题满分13分)
设 为坐标原点,
为坐标原点, ,
,
(1)若四边形 是平行四边形,求
是平行四边形,求 的大小;
的大小;
(2)在(1)的条件下,设 中点为
中点为 ,
, 与
与 交于
交于 ,求
,求 .
.
(1)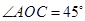 (2)
(2)
解析试题分析:(1)有题意: 由
由 得
得 …………………………………………………………(3分)
…………………………………………………………(3分)
所以
又
所以 ………………………………………..(6分)
………………………………………..(6分)
(2) 为
为 中点,
中点, 的坐标为
的坐标为
又由 ,故
,故 的坐标为
的坐标为 ……………………………………….(9分)
……………………………………….(9分)
所以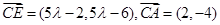
因为 三点共线,故
三点共线,故 ………………………………………………(11分)
………………………………………………(11分)
得 ,解得
,解得 ,从而
,从而 …………….(13分)
…………….(13分)
考点:利用向量求直线夹角及点的坐标
点评:题中利用平行四边形的性质转化为向量关系,进而代入点的坐标进行计算,当遇到三点共线时,转化为三点确定的两向量共线

练习册系列答案
相关题目
下列向量中,与向量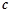
 不共线的一个向量
不共线的一个向量
 ( )
( )
A. | B. | C. | D. |
 的内角,
的内角, 分别是其对边长,向量
分别是其对边长,向量 ,
, ,
, .
.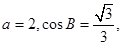 求
求 的长.
的长. 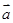 =(-1,1),
=(-1,1), =(x,3),
=(x,3), =(5,y),
=(5,y), =(8,6),且
=(8,6),且 ,
,
 ,且
,且 ∥(
∥( ),求x的值;
),求x的值; ,求实数
,求实数 的取值范围.
的取值范围. 、
、 ,
,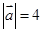 ,
, ,
, .
. 的值;
的值; ;
; 的值.
的值. ,
, ,求x,y的值使
,求x,y的值使 ,且
,且 。
。 ,函数
,函数
 的单调递减区间.
的单调递减区间. 的图象向左平移
的图象向左平移 个单位,再将所得图象上各点的横坐标缩短为原来的
个单位,再将所得图象上各点的横坐标缩短为原来的 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数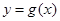 的图象.求
的图象.求 在
在
 上的值域.
上的值域.