题目内容
椭圆C: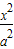 +
+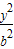 =1(a>b>0)的两个焦点为F1、F2,短轴两端点B1、B2,已知F1、F2、B1、B2四点共圆,且点N(0,3)到椭圆上的点最远距离为5
=1(a>b>0)的两个焦点为F1、F2,短轴两端点B1、B2,已知F1、F2、B1、B2四点共圆,且点N(0,3)到椭圆上的点最远距离为5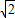 .
.(1)求此时椭圆C的方程;
(2)设斜率为k(k≠0)的直线m与椭圆C相交于不同的两点E、F,Q为EF的中点,问E、F两点能否关于过点P(0,
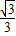 )、Q的直线对称?若能,求出k的取值范围;若不能,请说明理由.
)、Q的直线对称?若能,求出k的取值范围;若不能,请说明理由.
【答案】分析:(1)由F1、F2、B1、B2四点共圆,得出b=c,进而得到a2=b2+c2=2b2,再设椭圆的方程(含参数b),设H(x,y)为椭圆上一点,化简点(0,3)到椭圆上的点的距离,利用其最大值,分类讨论求出参数b的值,即得椭圆的方程.
(2)设直线L的方程为y=kx+m,代入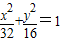 .由直线l与椭圆相交于不同的两点可得△>0即m2<32k2+16,要使A、B两点关于过点P、Q的直线对称,必须
.由直线l与椭圆相交于不同的两点可得△>0即m2<32k2+16,要使A、B两点关于过点P、Q的直线对称,必须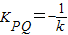 ,利用方程的根与系数的关系代入得
,利用方程的根与系数的关系代入得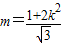 ,从而可求k得范围
,从而可求k得范围
解答:解:(1)∵F1、F2、B1、B2四点共圆,
∴b=c,
∴a2=b2+c2=2b2,
设椭圆的方程为 ,N(0,3)
,N(0,3)
设H(x,y)为椭圆上一点,则|HN|2=x2+(y-3)2=-(y+3)2+2b2+18,(-b≤y≤b),
①若0<b<3,|HN|2的最大值b2+6b+9=50得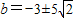 (舍去),
(舍去),
②若b≥3,|HN|2的最大值2b2+18=50得b2=16,
∴所求的椭圆的方程为: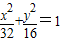 .
.
(2)设直线L的方程为y=kx+m,代入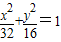 得(1+2k2)x2+4kmx+(2m2-32)=0.
得(1+2k2)x2+4kmx+(2m2-32)=0.
由直线l与椭圆相交于不同的两点知△=(4km)2-4(1+2k2)(2m2-32)>0,
m2<32k2+16.②
要使A、B两点关于过点P、Q的直线对称,必须
设A(x1,y1)B(x2,y2),则 ,
,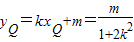
∵
解得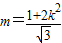 .③
.③
由②、③得
∴ ,
,
∵k2>0,
∴
∴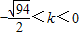 或0
或0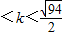
故当 或0
或0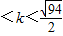 时,A、B两点关于过点P、Q的直线对称.
时,A、B两点关于过点P、Q的直线对称.
点评:本题主要考查了利用椭圆的性质求解椭圆的方程,直线与圆锥曲线的位置关系的综合应用,点关于直线的对称得性质的应用.椭圆的性质及其应用、函数最值的求法等,解题时要注意分类讨论思想的合理运用.
(2)设直线L的方程为y=kx+m,代入
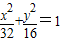 .由直线l与椭圆相交于不同的两点可得△>0即m2<32k2+16,要使A、B两点关于过点P、Q的直线对称,必须
.由直线l与椭圆相交于不同的两点可得△>0即m2<32k2+16,要使A、B两点关于过点P、Q的直线对称,必须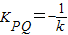 ,利用方程的根与系数的关系代入得
,利用方程的根与系数的关系代入得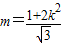 ,从而可求k得范围
,从而可求k得范围解答:解:(1)∵F1、F2、B1、B2四点共圆,
∴b=c,
∴a2=b2+c2=2b2,
设椭圆的方程为
 ,N(0,3)
,N(0,3)设H(x,y)为椭圆上一点,则|HN|2=x2+(y-3)2=-(y+3)2+2b2+18,(-b≤y≤b),
①若0<b<3,|HN|2的最大值b2+6b+9=50得
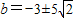 (舍去),
(舍去),②若b≥3,|HN|2的最大值2b2+18=50得b2=16,
∴所求的椭圆的方程为:
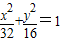 .
.(2)设直线L的方程为y=kx+m,代入
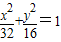 得(1+2k2)x2+4kmx+(2m2-32)=0.
得(1+2k2)x2+4kmx+(2m2-32)=0.由直线l与椭圆相交于不同的两点知△=(4km)2-4(1+2k2)(2m2-32)>0,
m2<32k2+16.②
要使A、B两点关于过点P、Q的直线对称,必须

设A(x1,y1)B(x2,y2),则
 ,
,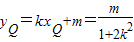
∵

解得
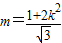 .③
.③由②、③得

∴
 ,
,∵k2>0,
∴

∴
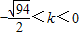 或0
或0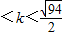
故当
 或0
或0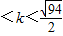 时,A、B两点关于过点P、Q的直线对称.
时,A、B两点关于过点P、Q的直线对称.点评:本题主要考查了利用椭圆的性质求解椭圆的方程,直线与圆锥曲线的位置关系的综合应用,点关于直线的对称得性质的应用.椭圆的性质及其应用、函数最值的求法等,解题时要注意分类讨论思想的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 +
+ =1(a>b>0),直线l为圆O:x2+y2=b2的一条切线,记椭圆C的离心率为e.
=1(a>b>0),直线l为圆O:x2+y2=b2的一条切线,记椭圆C的离心率为e. ,且恰好经过椭圆的右顶点,求e的大小;
,且恰好经过椭圆的右顶点,求e的大小; y+3=0相切,求椭圆方程.
y+3=0相切,求椭圆方程.
 +
+ =1(a>b>0)的左、右焦点分别为F
=1(a>b>0)的左、右焦点分别为F 、F
、F ,A是椭圆C上的一点,AF
,A是椭圆C上的一点,AF
 +y
+y ,y
,y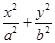 =1(a>b>0)的左、右焦点.
=1(a>b>0)的左、右焦点.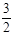 )到点F1、F2的距离之和等于4,求椭圆C的方程;
)到点F1、F2的距离之和等于4,求椭圆C的方程;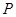 是(Ⅰ)中所得椭圆C上的动点,求线段
是(Ⅰ)中所得椭圆C上的动点,求线段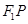 的中点
的中点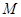 的轨迹方程.
的轨迹方程.