题目内容
【题目】已知等差数列{an}.满足:an+1>an(n∈N*),a1=1,该数列的前三项分别加上1,1,3后成等比数列,an+2log2bn=﹣1.
(Ⅰ)分别求数列{an},{bn}的通项公式;
(Ⅱ)求数列{anbn}的前n项和Tn .
【答案】解:(Ⅰ)设d、为等差数列{an}的公差,且d>0 由a1=1,a2=1+d,a3=1+2d,分别加上1,1,3成等比数列,
得(2+d)2=2(4+2d),
d>0,所以d=2,所以an=1+(n﹣1)×2=2n﹣1,
又因为an=﹣1﹣2log2bn ,
所以log2bn=﹣n即bn= ![]() .
.
(Ⅱ) ![]() …①,
…①,![]() …②,
…②,
① ﹣②,得![]() .
.
∴ 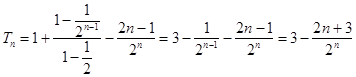
【解析】(Ⅰ)设d、为等差数列{an}的公差,且d>0,利用数列的前三项分别加上1,1,3后成等比数列,求出d,然后求解bn . (Ⅱ)写出 ![]() 利用错位相减法求和即可.
利用错位相减法求和即可.
【考点精析】本题主要考查了数列的前n项和的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系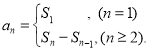 才能正确解答此题.
才能正确解答此题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

