题目内容
某次文艺汇演中共有9个展演节目,其中有两个是歌舞类节目,现随机安排演出表,则出现歌舞类节目即不在第一个,也不在最后一个,且不连续演出的概率为 .(结果用最简分数表示)
【答案】分析:根据条件可得满足条件的排法有 •A77 种,而所有的排法共有A99种不同的方法,由此求得所求事件的概率为
•A77 种,而所有的排法共有A99种不同的方法,由此求得所求事件的概率为  ,运算求得结果.
,运算求得结果.
解答:解:先把其余的7个节目任意排,共有A77种不同的方法,
再把两个歌舞类节目插入中间的6个空位中,共有A62种不同的方法.
故满足条件的排法有 •A77 种,而所有的排法共有A99种不同的方法.
•A77 种,而所有的排法共有A99种不同的方法.
故所求事件的概率为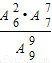 =
= =
=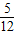 ,
,
故答案为: .
.
点评:本题考查等可能事件的概率,得到满足条件的排法有 •A77 种,是解题的关键,属于中档题.
•A77 种,是解题的关键,属于中档题.
 •A77 种,而所有的排法共有A99种不同的方法,由此求得所求事件的概率为
•A77 种,而所有的排法共有A99种不同的方法,由此求得所求事件的概率为  ,运算求得结果.
,运算求得结果.解答:解:先把其余的7个节目任意排,共有A77种不同的方法,
再把两个歌舞类节目插入中间的6个空位中,共有A62种不同的方法.
故满足条件的排法有
 •A77 种,而所有的排法共有A99种不同的方法.
•A77 种,而所有的排法共有A99种不同的方法.故所求事件的概率为
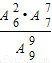 =
= =
=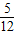 ,
,故答案为:
 .
.点评:本题考查等可能事件的概率,得到满足条件的排法有
 •A77 种,是解题的关键,属于中档题.
•A77 种,是解题的关键,属于中档题. 
练习册系列答案
相关题目