题目内容
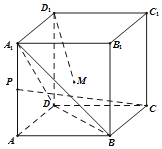
【题目】如图,正方体![]() 的棱长为1,
的棱长为1,![]() 为
为![]() 的中点,
的中点,![]() 在侧面
在侧面![]() 上,有下列四个命题:
上,有下列四个命题:
①若![]() ,则
,则![]() 面积的最小值为
面积的最小值为![]() ;
;
②平面![]() 内存在与
内存在与![]() 平行的直线;
平行的直线;
③过![]() 作平面
作平面![]() ,使得棱
,使得棱![]() ,
,![]() ,
,![]() 在平面
在平面![]() 的正投影的长度相等,则这样的平面
的正投影的长度相等,则这样的平面![]() 有4个;
有4个;
④过![]() 作面
作面![]() 与面
与面![]() 平行,则正方体
平行,则正方体![]() 在面
在面![]() 的正投影面积为
的正投影面积为![]() .
.
则上述四个命题中,真命题的个数为( )
A. 1B. 2C. 3D. 4
【答案】C
【解析】
①建立空间坐标系,得到![]() 点应该满足的条件,再根据二次函数的最值的求法求解即可;对于②
点应该满足的条件,再根据二次函数的最值的求法求解即可;对于②![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 也与平面
也与平面![]() 相交.故②错;对于③过
相交.故②错;对于③过![]() 作平面
作平面![]() ,使得棱
,使得棱![]() ,
,![]() ,
,![]() 在平面
在平面![]() 的正投影的长度相等,因为
的正投影的长度相等,因为![]() ,且
,且![]() ,所以
,所以![]() 在平面
在平面![]() 的正投影长度与
的正投影长度与![]() 在平面
在平面![]() 的正投影长度相等,然后分情况讨论即可得到平面
的正投影长度相等,然后分情况讨论即可得到平面![]() 的个数;对于④面
的个数;对于④面![]() 与面
与面![]() 平行,则正方体
平行,则正方体![]() 在面
在面![]() 的正投影为正六边形,且正六边形的边长为正三角形
的正投影为正六边形,且正六边形的边长为正三角形![]() 外接圆的半径,故其面积为
外接圆的半径,故其面积为![]() .
.
解:对于①,以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系,如图1所示;
轴,建立空间直角坐标系,如图1所示;
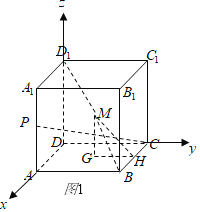
过![]() 作
作![]() 平面
平面![]() ,
,![]() 是垂足,过
是垂足,过![]() 作
作![]() ,交
,交![]() 于
于![]() ,连结
,连结![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴![]() ,
,![]() ,
,
![]()
![]() ,
,
∴![]()
![]() ,
,
当![]() 时,
时,![]() ,①正确;
,①正确;
对于![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 也与平面
也与平面![]() 相交.故②错;
相交.故②错;
③过![]() 作平面
作平面![]() ,使得棱
,使得棱![]() ,
,![]() ,
,![]() 在平面
在平面![]() 的正投影的长度相等,因为
的正投影的长度相等,因为![]() ,且
,且![]() ,故
,故![]() 在平面
在平面![]() 的正投影的长度等于
的正投影的长度等于![]() 在平面
在平面![]() 的正投影的长度,使得棱
的正投影的长度,使得棱![]() ,
,![]() ,
,![]() 在平面
在平面![]() 的正投影的长度相等,即使得使得棱
的正投影的长度相等,即使得使得棱![]() ,
,![]() ,
,![]() 面
面![]() 的正投影的长度相等,若棱
的正投影的长度相等,若棱![]() ,
,![]() ,
,![]() 面
面![]() 的同侧,则
的同侧,则![]() 为过
为过![]() 且与平面
且与平面![]() 平行的平面,若棱
平行的平面,若棱![]() ,
,![]() ,
,![]() 中有一条棱和另外两条棱分别在平面
中有一条棱和另外两条棱分别在平面![]() 的异侧,则这样的平面
的异侧,则这样的平面![]() 有3个,故满足使得棱
有3个,故满足使得棱![]() ,
,![]() ,
,![]() 在平面
在平面![]() 的正投影的长度相等的平面
的正投影的长度相等的平面![]() 有4个;③正确.
有4个;③正确.
④过![]() 作面
作面![]() 与面
与面![]() 平行,则正方体
平行,则正方体![]() 在面
在面![]() 的正投影为一个正六边形,其中
的正投影为一个正六边形,其中![]() 平面
平面![]() ,而
,而![]() 分别垂直于正三角形
分别垂直于正三角形![]() 和
和![]() ,所以根据对称性,正方体的8个顶点中,
,所以根据对称性,正方体的8个顶点中,![]() 在平面
在平面![]() 内的投影点重合与正六边形的中心,其它六个顶点投影恰是正六边形的六个顶点,且正六边形的边长等于正三角形
内的投影点重合与正六边形的中心,其它六个顶点投影恰是正六边形的六个顶点,且正六边形的边长等于正三角形![]() 的外接圆半径(投影线与正三角形
的外接圆半径(投影线与正三角形![]() 、
、![]() 垂直),所以正六边形的边长为
垂直),所以正六边形的边长为![]() ,所以投影的面积为
,所以投影的面积为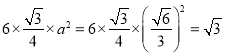 .④对.
.④对.
故选:C.

【题目】某公司计划购买1台机器,该种机器使用三年后即被淘汰.在购进机器时,可以一次性额外购买几次维修服务,每次维修服务费用200元,另外实际维修一次还需向维修人员支付小费,小费每次50元.在机器使用期间,如果维修次数超过购机时购买的维修服务次数,则每维修一次需支付维修服务费用500元,无需支付小费.现需决策在购买机器时应同时一次性购买几次维修服务,为此搜集并整理了100台这种机器在三年使用期内的维修次数,得下面统计表:
维修次数 | 8 | 9 | 10 | 11 | 12 |
频数 | 10 | 20 | 30 | 30 | 10 |
记x表示1台机器在三年使用期内的维修次数,y表示1台机器在维修上所需的费用(单位:元),![]() 表示购机的同时购买的维修服务次数.
表示购机的同时购买的维修服务次数.
(1)若![]() =10,求y与x的函数解析式;
=10,求y与x的函数解析式;
(2)若要求“维修次数不大于![]() ”的频率不小于0.8,求n的最小值;
”的频率不小于0.8,求n的最小值;
(3)假设这100台机器在购机的同时每台都购买10次维修服务,或每台都购买11次维修服务,分别计算这100台机器在维修上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买10次还是11次维修服务?
【题目】2019年4月,甲乙两校的学生参加了某考试机构举行的大联考,现对这两校参加考试的学生的数学成绩进行统计分析,数据统计显示,考生的数学成绩![]() 服从正态分布
服从正态分布![]() ,从甲乙两校100分及以上的试卷中用系统抽样的方法各抽取了20份试卷,并将这40份试卷的得分制作成如图所示的茎叶图:
,从甲乙两校100分及以上的试卷中用系统抽样的方法各抽取了20份试卷,并将这40份试卷的得分制作成如图所示的茎叶图:
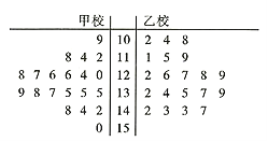
(1)试通过茎叶图比较这40份试卷的两校学生数学成绩的中位数;
(2)若把数学成绩不低于135分的记作数学成绩优秀,根据茎叶图中的数据,判断是否有![]() 的把握认为数学成绩在100分及以上的学生中数学成绩是否优秀与所在学校有关?
的把握认为数学成绩在100分及以上的学生中数学成绩是否优秀与所在学校有关?
(3)从所有参加此次联考的学生中(人数很多)任意抽取3人,记数学成绩在134分以上的人数为![]() ,求
,求![]() 的数学期望.
的数学期望.
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]()
![]() ,
,![]() .
.
参考公式与临界值表:![]() ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |