题目内容
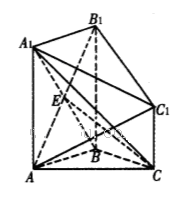
如图,在几何体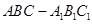 中,点
中,点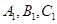 在平面ABC内的正投影分别为A,B,C,且
在平面ABC内的正投影分别为A,B,C,且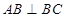 ,E为
,E为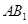 中点,
中点,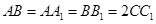 .
.
(1)求证;CE∥平面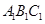 ,
,
(2)求证:平面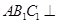 平面
平面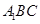
详见解析
解析试题分析:(1)通过证明线线平行,证明线面平行,所以取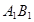 的中点
的中点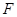 ,连接
,连接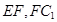 ,通过证明
,通过证明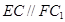 ,从而证明
,从而证明 ;(2)根据已知条件:
;(2)根据已知条件: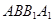 为正方形,证出
为正方形,证出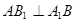 ,
,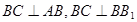 ,所以
,所以 ,所以
,所以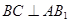 ,得出
,得出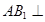 面
面 ,
,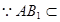 面
面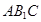 ,
, 平面
平面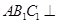 平面
平面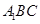 . 证明平行和垂直都是最基本的证明问题,要熟练掌握判定定理,可以由结论出发,逐步找到证明的充分条件,然后再逻辑顺序写出证明过程,属于中档题.
. 证明平行和垂直都是最基本的证明问题,要熟练掌握判定定理,可以由结论出发,逐步找到证明的充分条件,然后再逻辑顺序写出证明过程,属于中档题.
试题解析:(1)由题意知: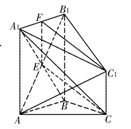
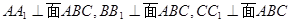
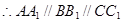 1分
1分
取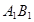 中点
中点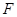 ,连
,连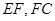 ,
,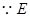 为
为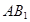 中点,
中点,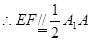
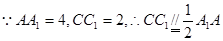
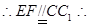 四边形
四边形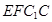 为平行四边形
为平行四边形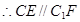 4分
4分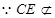 面
面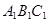 ,
,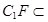 面
面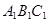
 面
面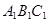 6分
6分
(2)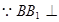 面
面 ,
,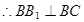
又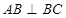 ,
,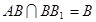 ,
,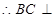 面
面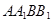 8分
8分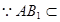 面
面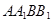 ,
,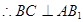
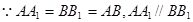
 四边形
四边形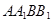 为正方形,
为正方形,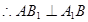 10分
10分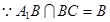 ,
,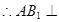 面
面
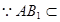 面
面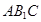
 平面
平面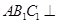 平面
平面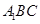 12分
12分
考点:1.线面平行的判定定理;2.面面垂直的判断.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
 .
.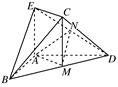
 平面
平面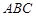 ,四边形
,四边形 为矩形,△
为矩形,△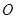 为
为 的中点,
的中点,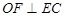 .
.
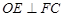 ;
; 的正切值.
的正切值.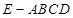 中,底面
中,底面 是正方形,
是正方形,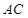 与
与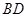 交于点
交于点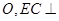 底面
底面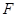 为
为 的中点.
的中点.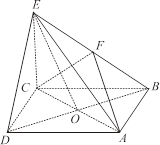
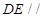 平面
平面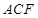 ;
; ,在线段
,在线段 上是否存在点
上是否存在点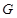 ,使
,使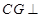 平面
平面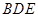 ?若存在,求出
?若存在,求出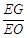 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.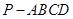 中,底面
中,底面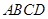 是边长为2的正方形,侧面
是边长为2的正方形,侧面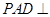 底面
底面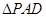 为等腰直角三角形,
为等腰直角三角形,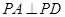 ,
,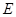 、
、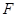 分别为
分别为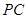 、
、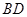 的中点.
的中点.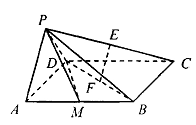
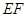 //平面
//平面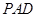 ;
; 中点为
中点为 ,求二面角
,求二面角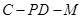 的余弦值.
的余弦值.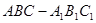 中,
中, ,
, ,异面直线
,异面直线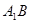 与
与 所成的角等于
所成的角等于 ,设
,设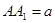 .
.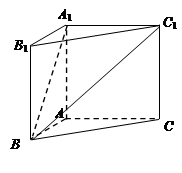
 的值;
的值; 与平面
与平面 所成的锐二面角的大小.
所成的锐二面角的大小. ACD沿AC折起至
ACD沿AC折起至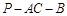 为600,G,H分别是PA,PC的中点.
为600,G,H分别是PA,PC的中点.
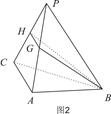
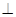 平面BGH;
平面BGH; =1.
=1.
 ?若存在,求出CM的长;若不存在,请说明理由.
?若存在,求出CM的长;若不存在,请说明理由.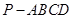 中,底面
中,底面 为菱形,
为菱形, 平面
平面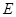 为
为 的中点,
的中点,
 平面
平面 ; (II)平面
; (II)平面 ⊥平面
⊥平面 .
.