题目内容
【题目】记无穷数列![]() 的前n项中最大值为
的前n项中最大值为![]() ,最小值为
,最小值为![]() ,令
,令![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() .
.
(1)若数列![]() 是首项为2,公比为2的等比数列,求
是首项为2,公比为2的等比数列,求![]() ;
;
(2)若数列![]() 是等差数列,试问数列
是等差数列,试问数列![]() 是否也一定是等差数列?若是,请证明;若不是,请举例说明;
是否也一定是等差数列?若是,请证明;若不是,请举例说明;
(3)若![]() ,求
,求![]() .
.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() ,
,![]()
【解析】
(1)由题意求得![]() 和
和![]() ,即得
,即得![]() ,利用等比数列求和公式可得结果.
,利用等比数列求和公式可得结果.
(2)若“数列{bn}是等差数列”,设其公差为d′,bn+1﹣bn![]() d′,根据定义,Mn+1≥Mn,mn+1≤mn,至少有一个取等号,当d′>0时,Mn+1>Mn,an+1=Mn+1>Mn≥an,即数列{an}为增数列,则Mn=an,mn=a1,进而得出.同理可得d′<0时,“数列{an}是等差数列”;当d′=0时,Mn+1=Mn,且mn+1=mn,故{an}为常数列,是等差数列.
d′,根据定义,Mn+1≥Mn,mn+1≤mn,至少有一个取等号,当d′>0时,Mn+1>Mn,an+1=Mn+1>Mn≥an,即数列{an}为增数列,则Mn=an,mn=a1,进而得出.同理可得d′<0时,“数列{an}是等差数列”;当d′=0时,Mn+1=Mn,且mn+1=mn,故{an}为常数列,是等差数列.
(3)由题意可得![]() ,根据定义可以分析得到当
,根据定义可以分析得到当![]() 时,
时,![]() ,即得
,即得![]() ;同理可得
;同理可得![]() 时,
时,![]() .,
.,
所以当![]() 时,
时,![]() ,
,![]() 得到
得到![]() 可得
可得![]() ,求得
,求得
![]() ;当
;当![]() 时,
时,![]() 得到
得到![]() ,求得
,求得![]() ,分段写出结果即可.
,分段写出结果即可.
(1)∵数列![]() 是首项为2,公比为2的等比数列,∴
是首项为2,公比为2的等比数列,∴![]() ,∴
,∴![]() ,
,![]()
则![]() ,∴
,∴![]()
(2)若数列![]() 是等差数列,设其公差为
是等差数列,设其公差为![]()
∵![]()
![]()
根据![]() ,
,![]() 的定义,有以下结论:
的定义,有以下结论:
![]() ,
,![]() ,且两个不等式中至少有一个取等号,
,且两个不等式中至少有一个取等号,
①若![]() ,则必有
,则必有![]() ,∴
,∴![]() ,即对
,即对![]() ,
,![]() ,都有
,都有![]()
∴![]() ,
,![]() ,
,![]()
![]()
∴![]() ,即
,即![]() 为等差数列;
为等差数列;
②当![]() 时,则必有
时,则必有![]() ,所以
,所以![]() ,即对
,即对![]() ,
,![]() ,都有
,都有![]()
∴![]() ,
,![]() ,
,![]()
![]()
所以![]() ,即
,即![]() 为等差数列;
为等差数列;
③当![]() ,
,![]()
![]()
∵![]() ,
,![]() 中必有一个为0,∴根据上式,一个为0,则另一个亦为0,
中必有一个为0,∴根据上式,一个为0,则另一个亦为0,
即![]() ,
,![]() ,∴
,∴![]() 为常数数列,所以
为常数数列,所以![]() 为等差数列,
为等差数列,
综上,数列![]() 也一定是等差数列.
也一定是等差数列.
(3)∵![]() ,
,
∴当![]() 时,
时,![]() ,即
,即![]() ,当
,当![]() 时,
时,![]() ,即
,即![]() .
.
以下证明:![]() ,
,![]()
当![]() 时,
时,
若![]() ,则
,则![]() ,
,![]() ,所以
,所以![]() ,不合题意;
,不合题意;
若![]() ,则
,则![]() ,
,![]() ,则
,则![]() ,得:
,得:![]() ,与
,与![]() 矛盾,不合题意;
矛盾,不合题意;
∴![]() ,即
,即![]() ;
;
同理可证:![]() ,即
,即![]() ,
,![]() 时,
时,![]() .
.
①当![]() 时,
时,![]() ,
,![]() ∴
∴![]() ∴
∴![]() ,
,![]()
∵![]() ∴
∴![]()
∴![]()
![]()
②当![]() 时,
时,![]() ,且
,且![]()
∴![]() ,则
,则![]() 为
为![]() 或
或![]() .若
.若![]() 为
为![]() ,则
,则![]() 为常数,与题意不符,∴
为常数,与题意不符,∴![]() ∴
∴![]() ∴
∴![]()
∴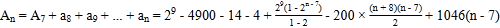
![]() ,
,
∴![]() ,
,![]() .
.

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案【题目】2019年春节档有多部优秀电影上映,其中《流浪地球》是比较火的一部.某影评网站统计了100名观众对《流浪地球》的评分情况,得到如下表格:
评价等级 | ★ | ★★ | ★★★ | ★★★★ | ★★★★★ |
分数 | 0~20 | 2140 | 4160 | 61~80 | 81100 |
人数 | 5 | 2 | 12 | 6 | 75 |
(1)根据以上评分情况,试估计观众对《流浪地球》的评价在四星以上(包括四星)的频率;
(2)以表中各评价等级对应的频率作为各评价等级对应的概率,假设每个观众的评分结果相互独立.
(i)若从全国所有观众中随机选取3名,求恰有2名评价为五星1名评价为一星的概率;
(ii)若从全国所有观众中随机选取16名,记评价为五星的人数为X,求X的方差.
【题目】柴静《穹顶之下》的播出,让大家对雾霾天气的危害有了更进一步的认识,对于雾霾天气的研究也渐渐活跃起来,某研究机构对春节燃放烟花爆竹的天数x与雾霾天数y进行统计分析,得出下表数据:
x | 4 | 5 | 7 | 8 |
y | 2 | 3 | 5 | 6 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)试根据(2)求出的线性回归方程,预测燃放烟花爆竹的天数为![]() 的雾霾天数.
的雾霾天数.