题目内容
(本小题满分12分)
已知四棱锥 的三视图如图所示,
的三视图如图所示, 为正三角形.
为正三角形.

(Ⅰ)在平面 中作一条与底面
中作一条与底面 平行的直线,并说明理由;
平行的直线,并说明理由;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)求三棱锥 的高.
的高.
(Ⅰ)分别取 中点
中点 ,连结
,连结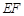 ,则
,则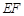 即为所求,下证之:·········· 1分
即为所求,下证之:·········· 1分

∵  分别为
分别为 中点,
中点,
∴  .················································ 2分
.················································ 2分
∵  平面
平面 ,
, 平面
平面 ,··· 3分
,··· 3分
∴  平面
平面 .··································· 4分
.··································· 4分
(作法不唯一)
(Ⅱ)见解析;(Ⅲ)  .
.
【解析】(I)在平面PCD内作一条与CD平行的直线即可.可以考虑作三角形PCD的中位线.
(II)由于PA垂直AC,所以只须证AC垂直AB即可.可以利用勾股定理进行证明.
(III)求三棱锥的高可以考虑其特殊性,采用换底的方法利用体积法求解是一条比较好的求解方法.本小题可以考虑利用 进行求解.
进行求解.
(Ⅰ)分别取 中点
中点 ,连结
,连结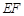 ,则
,则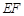 即为所求,下证之:·········· 1分
即为所求,下证之:·········· 1分

∵  分别为
分别为 中点,
中点,
∴  .················································ 2分
.················································ 2分
∵  平面
平面 ,
, 平面
平面 ,··· 3分
,··· 3分
∴  平面
平面 .··································· 4分
.··································· 4分
(作法不唯一)
(Ⅱ)由三视图可知, 平面
平面 ,
, ,四边形
,四边形 为直角梯形.
为直角梯形.
过点 作
作 于
于 ,则
,则 ,
, .
.
∴ 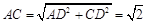 ,
, ,
,
∴  ,故
,故 .······························································· 6分
.······························································· 6分
∵  平面
平面 ,
, 平面
平面 ,
,
∴  .···································································································· 7分
.···································································································· 7分
∵  ,
,
∴  平面
平面 .······················································································· 8分
.······················································································· 8分
(Ⅲ)∵  为正三角形,
为正三角形,
∴  .
.
在 中,
中, .
.
∴  ,··································· 10分
,··································· 10分
 (其中
(其中 为三棱锥
为三棱锥 的高).
的高).
························································································································ 11分
∵  ,
,
∴  . 12分
. 12分

 名校课堂系列答案
名校课堂系列答案