题目内容
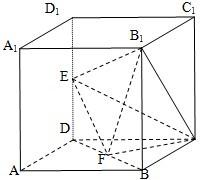 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1、DB的中点.
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1、DB的中点.(Ⅰ)求证:EF∥平面ABC1D1;
(Ⅱ)求证:EF⊥B1C.
分析:(I)欲证EF∥平面ABC1D1,根据直线与平面平行的判定定理可知只需证EF与平面ABC1D1内一直线平行即可,连接BD1,在△DD1B中,E、F分别为D1D,DB的中点,则EF∥D1B,而D1B?平面ABC1D1,EF?平面ABC1D1,满足定理所需条件;
(II)欲证EF⊥B1C,可先证B1C⊥面ABC1D1,根据直线与平面垂直的判定定理可知只需证B1C与面ABC1D1内两相交直线垂直,而B1C⊥AB,B1C⊥BC1,满足定理条件,问题即可得证.
(II)欲证EF⊥B1C,可先证B1C⊥面ABC1D1,根据直线与平面垂直的判定定理可知只需证B1C与面ABC1D1内两相交直线垂直,而B1C⊥AB,B1C⊥BC1,满足定理条件,问题即可得证.
解答: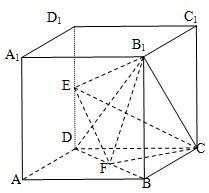 证明:(Ⅰ)连接BD1,在△DD1B中,E、F分别为D1D,DB的中点,则
证明:(Ⅰ)连接BD1,在△DD1B中,E、F分别为D1D,DB的中点,则
?EF∥平面ABC1D1;
(Ⅱ)根据题意可知:
?
?
?EF⊥B1C.
 证明:(Ⅰ)连接BD1,在△DD1B中,E、F分别为D1D,DB的中点,则
证明:(Ⅰ)连接BD1,在△DD1B中,E、F分别为D1D,DB的中点,则
|
(Ⅱ)根据题意可知:
|
|
?
|
点评:本题考查直线与平面平行的判定,以及空间两直线的位置关系的判定,考查学生空间想象能力,逻辑思维能力,是中档题.

练习册系列答案
相关题目
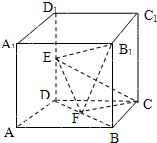 17、如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1,DB的中点
17、如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1,DB的中点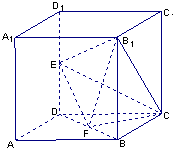 如图所示,在棱长为2的正方体中,E、F分别为DD1、BD的中点.
如图所示,在棱长为2的正方体中,E、F分别为DD1、BD的中点. 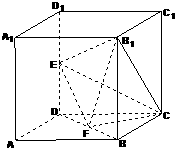 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.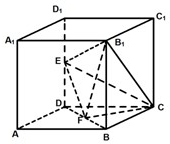 (2012•虹口区三模)如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.
(2012•虹口区三模)如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.