题目内容
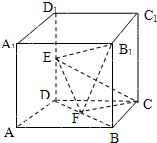 17、如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1,DB的中点
17、如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1,DB的中点(1)求证:EF∥平面ABC1D1;
(2)求二面角B1-EF-C的大小.
分析:(1)连BD1,因为E,F分别为DD1,DB的中点,由三角形的中位线的性质,我们易得EF∥BD1,进而根据线面平行的判定定理,得到EF∥平面ABC1D1;
(2)由在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1,DB的中点,我们易得面CEF⊥面B1EF,根据直二面角的定义,易得到二面角B1-EF-C的大小.
(2)由在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1,DB的中点,我们易得面CEF⊥面B1EF,根据直二面角的定义,易得到二面角B1-EF-C的大小.
解答: 解:(1)连BD1,因为E,F分别为DD1,DB的中点,?EF∥BD1,又EF?面ABC1D1,BD1?面ABC1D1,所以,EF∥面ABC1D1.
解:(1)连BD1,因为E,F分别为DD1,DB的中点,?EF∥BD1,又EF?面ABC1D1,BD1?面ABC1D1,所以,EF∥面ABC1D1.
(2)∵F为BD的中点,?CF⊥BD,又CF⊥BB1,?CF⊥面BB1D1D,?面CEF⊥面BB1D1D,?面CEF⊥面B1EF,∴二面角B1-EF-C的大小为90°.
 解:(1)连BD1,因为E,F分别为DD1,DB的中点,?EF∥BD1,又EF?面ABC1D1,BD1?面ABC1D1,所以,EF∥面ABC1D1.
解:(1)连BD1,因为E,F分别为DD1,DB的中点,?EF∥BD1,又EF?面ABC1D1,BD1?面ABC1D1,所以,EF∥面ABC1D1.(2)∵F为BD的中点,?CF⊥BD,又CF⊥BB1,?CF⊥面BB1D1D,?面CEF⊥面BB1D1D,?面CEF⊥面B1EF,∴二面角B1-EF-C的大小为90°.
点评:本题考查的知识点是平面与平面垂直的判定,直线与平面平行的判定,其中熟练掌握空间线面平行和垂直的判定定理及性质定理,是解答此类问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
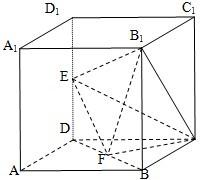 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1、DB的中点.
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1、DB的中点.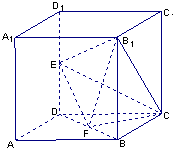 如图所示,在棱长为2的正方体中,E、F分别为DD1、BD的中点.
如图所示,在棱长为2的正方体中,E、F分别为DD1、BD的中点. 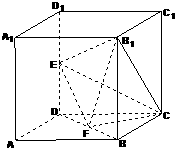 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.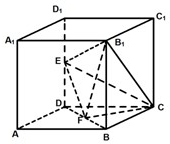 (2012•虹口区三模)如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.
(2012•虹口区三模)如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.