题目内容
如图所示,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,AB=2,PA=2 ,M是PA的中点.
,M是PA的中点.(1)求证:平面PCD∥平面MBE;
(2)求四棱锥M-BCDE的体积.

【答案】分析:(1)证明平面PCD∥平面MBE,利用面面平行的判定定理,证明一个平面内的两条相交直线平行于另一平面即可;
(2)利用M是PA的中点,说明所求棱锥的高,求出底面面积,然后求出棱锥的体积即可.
解答:解:(1)证明:连接AD交BE于点G,连接MG,则点G是正六边形的中心,所以G是线段AD的中点
∵M是PA的中点,∴MG∥PD
∵PD?平面MBE,MG?平面MBE
∴PD∥平面MBE
∵DC∥BE,DC?平面MBE,BE?平面MBE
∴DC∥平面MBE
∵PD∩DC=D
∴平面PCD∥平面MBE;
(2)因为六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,AB=2,PA=2 ,M是PA的中点,
,M是PA的中点,
所以所求棱锥的高为 ,底面面积为
,底面面积为 =3
=3 .
.
所以所求棱锥的体积为: =
= .
.
点评:本题考查平面与平面平行的判断方法,几何体的体积的求法,考查空间想象能力计算能力.
(2)利用M是PA的中点,说明所求棱锥的高,求出底面面积,然后求出棱锥的体积即可.
解答:解:(1)证明:连接AD交BE于点G,连接MG,则点G是正六边形的中心,所以G是线段AD的中点
∵M是PA的中点,∴MG∥PD
∵PD?平面MBE,MG?平面MBE
∴PD∥平面MBE
∵DC∥BE,DC?平面MBE,BE?平面MBE
∴DC∥平面MBE
∵PD∩DC=D
∴平面PCD∥平面MBE;
(2)因为六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,AB=2,PA=2
 ,M是PA的中点,
,M是PA的中点,所以所求棱锥的高为
 ,底面面积为
,底面面积为 =3
=3 .
.所以所求棱锥的体积为:
 =
= .
.点评:本题考查平面与平面平行的判断方法,几何体的体积的求法,考查空间想象能力计算能力.

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目


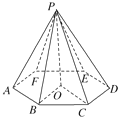 如图所示,已知六棱锥P-ABCDEF,其中底面ABCDEF是正六边形,点P在底面的投影是正六边形的中心,底面边长为2cm,侧棱长为3cm,求六棱锥P-ABCDEF的表面积和体积.
如图所示,已知六棱锥P-ABCDEF,其中底面ABCDEF是正六边形,点P在底面的投影是正六边形的中心,底面边长为2cm,侧棱长为3cm,求六棱锥P-ABCDEF的表面积和体积. 的底面是正六边形,
的底面是正六边形, 平面
平面 ,
, 是
是 的中点。
的中点。
 //平面
//平面 ;
; ,当二面角
,当二面角 的大小为
的大小为 时,求
时,求 的值。
的值。 ,M是PA的中点.
,M是PA的中点.