题目内容
.(10分)已知集合A={x|>1,x∈R},B={x|x2-2x-m<0},
(1)当m=3时,求A∩(∁RB);
(2)若A∩B={x|-1<x<4},求实数m的值.
【答案】
解 由>1,得<0.
∴-1<x<5,∴A={x|-1<x<5}.
(1)当m=3时,B={x|-1<x<3},
则∁RB={x|x≤-1或x≥3},
∴A∩(∁RB)={x|3≤x<5}.
(2)∵A={x|-1<x<5},A∩B={x|-1<x<4},
∴有42-2×4-m=0,解得m=8.
此时B={x|-2<x<4},符合题意,故实数m的值为8
【解析】略

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
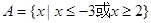 ,
,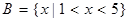 ,
,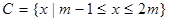
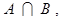
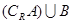
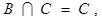 求实数m的取值范围。
求实数m的取值范围。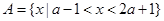 ,
,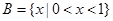 ,若
,若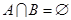 ,求实数a的取值范围.
,求实数a的取值范围. 是满足下列性质的函数
是满足下列性质的函数 的全体:在定义域内存在
的全体:在定义域内存在 ,使得
,使得 成立.
成立.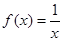 是否属于集合
是否属于集合 ,求实数
,求实数 的取值范围.
的取值范围.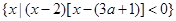 ,B=
,B=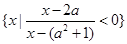 .
.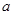 =2时,求A
=2时,求A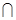 B; (2)求使B
B; (2)求使B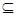 A的实数
A的实数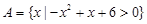 ,
,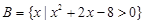 ,求
,求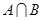 .
.